
【题目】设函数![]() (a,b
(a,b![]() R)的导函数为
R)的导函数为![]() ,已知
,已知![]() ,
,![]() 是
是![]() 的两个不同的零点.
的两个不同的零点.
(1)证明:![]() ;
;
(2)当b=0时,若对任意x>0,不等式![]() 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(3)求关于x的方程![]() 的实根的个数.
的实根的个数.
【答案】(1)见解析;(2)![]() ;(3)1个.
;(3)1个.
【解析】
(1)求函数的导数,利用△=4a2﹣12b>0,得证;
(2)分离参数a,所以a≥![]() ﹣x对任意x>0恒成立,令新函数设g(x)=
﹣x对任意x>0恒成立,令新函数设g(x)=![]() ﹣x求最值即可,或采用x3+ax2﹣xlnx≥0时求左侧最值亦可.
﹣x求最值即可,或采用x3+ax2﹣xlnx≥0时求左侧最值亦可.
(3)转化函数求零点个数可得结论.
(1)函数f(x)=x3+ax2+bx(a,b∈R)的导函数为f′(x)=3x2+2ax+b.
已知x1,x2是f'(x)的两个不同的零点,设x1<x2,
所以△=4a2﹣12b>0,所以:a2>3b得证;
(2)当b=0时,对任意x>0,f(x)≥xlnx恒成立,
所以x3+ax2≥xlnx,即x3+ax2﹣xlnx≥0,x2+ax﹣lnx≥0对任意x>0恒成立,
所以a≥![]() ﹣x对任意x>0恒成立,
﹣x对任意x>0恒成立,
设g(x)=![]() ﹣x,则
﹣x,则![]() ,
,
令h(x)=1﹣1nx﹣x2,则h![]() (x)=﹣
(x)=﹣![]() ﹣2x<0,
﹣2x<0,
所以h(x)在(0,+∞)上单调递减,注意到h(1)=0,
当x∈(0,1)时,h(x)>0,g![]() (x)>0,所以g(x)在(0,1)上单调递增,
(x)>0,所以g(x)在(0,1)上单调递增,
当x∈(1,+∞)时,H(x)<0,g![]() (x)<0,所以g(x)在(1,+∞)上单调递减,
(x)<0,所以g(x)在(1,+∞)上单调递减,
所以,当x=1时,g(x)有最大值g(1)=﹣1,
所以a的取值范围为[﹣1,+∞);
(3)由题意设F(x)=f(x)﹣f(x1)﹣![]() ,
,
则原问题转化为求函数F(x)的零点的个数,
因为导函数为f![]() (x)=3x2+2ax+b,已知x1,x2是f'(x)的两个不同的零点,
(x)=3x2+2ax+b,已知x1,x2是f'(x)的两个不同的零点,
所以:![]() ,所以:
,所以:
![]() ,
,
所以F(x)在(0,+∞)上单调递增,注意到F(x1)=0,所以F(x)在(0,+∞)上存在唯一零点x1,
∴关于x的方程![]() 有1个实根,
有1个实根,


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知某商品每件的生产成本![]() (元)与销售价格
(元)与销售价格![]() (元)具有线性相关关系,对应数据如表所示:
(元)具有线性相关关系,对应数据如表所示:
| 5 | 6 | 7 | 8 |
| 15 | 17 | 21 | 27 |
(1)求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若该商品的月销售量![]() (千件)与生产成本
(千件)与生产成本![]() (元)的关系为
(元)的关系为![]() ,
,![]() ,根据(1)中求出的线性回归方程,预测当
,根据(1)中求出的线性回归方程,预测当![]() 为何值时,该商品的月销售额最大.
为何值时,该商品的月销售额最大.
附: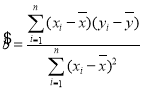 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,
,![]() 是长轴的一个端点,弦
是长轴的一个端点,弦![]() 过椭圆的中心
过椭圆的中心![]() ,点
,点![]() 在第一象限,且
在第一象限,且![]() ,
,![]() .
.
(1)求椭圆的标准方程;
(2)设![]() 、
、![]() 为椭圆上不重合的两点且异于
为椭圆上不重合的两点且异于![]() 、
、![]() ,若
,若![]() 的平分线总是垂直于
的平分线总是垂直于![]() 轴,问是否存在实数
轴,问是否存在实数![]() ,使得
,使得![]() ?若不存在,请说明理由;若存在,求
?若不存在,请说明理由;若存在,求![]() 取得最大值时的
取得最大值时的![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 是坐标原点.
是坐标原点.
(1)若直线![]() 过点
过点![]() 且
且![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)已知点![]() ,若直线
,若直线![]() 不与坐标轴垂直,且
不与坐标轴垂直,且![]() ,证明:直线
,证明:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0),四点P1(1,1),P2(0,1),P3(–1,
(a>b>0),四点P1(1,1),P2(0,1),P3(–1, ![]() ),P4(1,
),P4(1, ![]() )中恰有三点在椭圆C上.
)中恰有三点在椭圆C上.
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为–1,证明:l过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
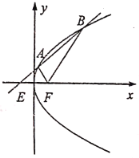
【题目】如图,已知F是抛物线C:![]() 的焦点,过E(﹣l,0)的直线
的焦点,过E(﹣l,0)的直线![]() 与抛物线分別交于A,B两点(点A,B在x轴的上方).
与抛物线分別交于A,B两点(点A,B在x轴的上方).
(1)设直线AF,BF的斜率分別为![]() ,
,![]() ,证明:
,证明:![]() ;
;
(2)若![]() ABF的面积为4,求直线
ABF的面积为4,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省确定从2021年开始,高考采用“![]() ”的模式,取消文理分科,即“3”包括语文、数学、英语,为必考科目:“1”表示从物理、历史中任选一门;“2”则是从生物、化学、地理、政治中选择两门,共计六门考试科目.某高中从高一年级2000名学生(其中女生900人)中,采用分层抽样的方法抽取
”的模式,取消文理分科,即“3”包括语文、数学、英语,为必考科目:“1”表示从物理、历史中任选一门;“2”则是从生物、化学、地理、政治中选择两门,共计六门考试科目.某高中从高一年级2000名学生(其中女生900人)中,采用分层抽样的方法抽取![]() 名学生进行调查.
名学生进行调查.
(1)已知抽取的![]() 名学生中含男生110人,求
名学生中含男生110人,求![]() 的值及抽取到的女生人数;
的值及抽取到的女生人数;
(2)学校计划在高二上学期开设选修中的“物理”和“历史”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的![]() 名学生讲行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目).下表是根据调查结果得到的
名学生讲行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目).下表是根据调查结果得到的![]() 列联表,请将列联表补充完整,并判断是否有
列联表,请将列联表补充完整,并判断是否有![]() 的把握认为选择科目与性别有关?说明你的理由;
的把握认为选择科目与性别有关?说明你的理由;
性别 | 选择物理 | 选择历史 | 总计 |
男生 | 50 | ||
女生 | 30 | ||
总计 |
(3)在(2)的条件下,从抽取的选择“物理”的学生中按分层抽样抽取6人,再从这6名学生中抽取2人,对“物理”的选课意向作深入了解,求2人中至少有1名女生的概率.
参考公式:![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
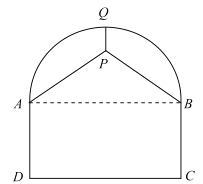
【题目】如图,某隧道的剖面图是由半圆及矩形![]() 组成,交通部门拟在隧道顶部安装通风设备(视作点
组成,交通部门拟在隧道顶部安装通风设备(视作点![]() ),为了固定该设备,计划除从隧道最高点
),为了固定该设备,计划除从隧道最高点![]() 处使用钢管垂直向下吊装以外,再在两侧自
处使用钢管垂直向下吊装以外,再在两侧自![]() 两点分别使用钢管支撑.已知道路宽
两点分别使用钢管支撑.已知道路宽![]() ,设备要求安装在半圆内部,所使用的钢管总长度为
,设备要求安装在半圆内部,所使用的钢管总长度为![]() .
.
(1)①设![]() ,将
,将![]() 表示为关于
表示为关于![]() 的函数;
的函数;
②设![]() ,将
,将![]() 表示为关于
表示为关于![]() 的函数;
的函数;
(2)请选用(1)中的一个函数关系式,说明如何设计,所用的钢管材料最省?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com