
【题目】若函数f(x)=x3﹣3a2x+1的图像与直线y=3只有一个公共点,则实数a的取值范围 .
科目:高中数学 来源: 题型:
【题目】如图,正三棱锥A﹣BCD的侧棱长为2,底面BCD的边长为2 ![]() ,E,分别为BC,BD的中点,则三棱锥A﹣BEF的外接球的半径R= , 内切球半径r= .
,E,分别为BC,BD的中点,则三棱锥A﹣BEF的外接球的半径R= , 内切球半径r= . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,则( )
A.f(x)在(0,+∞)上是增函数
B.f(x)在 ![]() 上是增函数
上是增函数
C.当x∈(0,1)时,f(x)有最小值 ![]()
D.f(x)在定义域内无极值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平行四边形ABCD(如图1),AB=4,AD=2,∠DAB=60°,E为AB的中点,把三角形ADE沿DE折起至A1DE位置,使得A1C=4,F是线段A1C的中点(如图2). 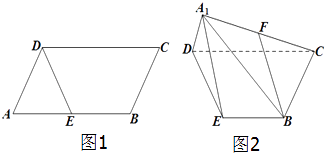
(1)求证:BF∥面A1DE;
(2)求证:面A1DE⊥面DEBC;
(3)求二面角A1﹣DC﹣E的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中 ①若loga3>logb3,则a>b;
②函数f(x)=x2﹣2x+3,x∈[0,+∞)的值域为[2,+∞);
③设g(x)是定义在区间[a,b]上的连续函数.若g(a)=g(b)>0,则函数g(x)无零点;
④函数 ![]() 既是奇函数又是减函数.
既是奇函数又是减函数.
其中正确的命题有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣3mx+n(m>0)的两个零点分别为1和2.
(1)求m、n的值;
(2)若不等式f(x)﹣k>0在x∈[0,5]恒成立,求k的取值范围.
(3)令 ![]() ,若函数F(x)=g(2x)﹣r2x在x∈[﹣1,1]上有零点,求实数r的取值范围.
,若函数F(x)=g(2x)﹣r2x在x∈[﹣1,1]上有零点,求实数r的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com