
【题目】若函数![]() 对定义域内的每一个值
对定义域内的每一个值![]() ,在其定义域内都存在唯一的
,在其定义域内都存在唯一的![]() ,使
,使![]() 成立,则称该函数为“依赖函数”.
成立,则称该函数为“依赖函数”.
(1)判断函数![]() 是否为“依赖函数”,并说明理由;
是否为“依赖函数”,并说明理由;
(2)若函数![]() 在定义域
在定义域![]() (
(![]() )上为“依赖函数”,求
)上为“依赖函数”,求![]() 的取值范围;
的取值范围;
(3)已知函数![]() 在定义域
在定义域![]() 上为“依赖函数”.若存在实数
上为“依赖函数”.若存在实数![]() ,使得对任意的
,使得对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
【答案】(1)不是“依赖函数”,见解析;(2)![]() (3)实数
(3)实数![]() 的最大值为
的最大值为![]() .
.
【解析】
(1)利用![]() 时,
时,![]() 不可能成立,判断出
不可能成立,判断出![]() 不是“依赖函数”.
不是“依赖函数”.
(2)结合指数型函数的单调性,利用“依赖函数”的定义,求得![]() ,由此将
,由此将![]() 转化为
转化为![]() ,然后结合二次函数的单调性,求得
,然后结合二次函数的单调性,求得![]() 的取值范围.
的取值范围.
(3)根据![]() 与区间
与区间![]() 的位置关系进行分类讨论,结合二次函数的性质以及“依赖函数”的定义,求得
的位置关系进行分类讨论,结合二次函数的性质以及“依赖函数”的定义,求得![]() 的值.由此化简不等式
的值.由此化简不等式![]() 为以
为以![]() 为主变量的形式.利用判别式得到
为主变量的形式.利用判别式得到![]() ,结合存在性问题,由
,结合存在性问题,由![]() 的最大值,求得
的最大值,求得![]() 的取值范围,从而求得
的取值范围,从而求得![]() 的最大值.
的最大值.
(1)对于函数![]() 的定义域
的定义域![]() 内存在
内存在![]() ,
,
则![]() ,无解,故
,无解,故![]() 不是“依赖函数”.
不是“依赖函数”.
(2)因为![]() 在
在![]() 递增,故
递增,故![]() ,即
,即![]() ,
,![]()
由![]() ,故
,故![]() ,得
,得![]() ,
,
从而![]() 在
在![]() 上单调递增,故
上单调递增,故![]() ,
,
(3)①若![]() ,故
,故![]() 在
在![]() 上最小值为0,此时不存在
上最小值为0,此时不存在![]() ,舍去;
,舍去;
②若![]() 故
故![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,解得
,解得![]() (舍)或
(舍)或![]() .
.
∴存在![]() ,使得对任意的
,使得对任意的![]() ,有不等式
,有不等式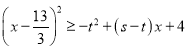 都成立,
都成立,
即![]() 恒成立,由
恒成立,由![]() ,
,
得![]() ,由
,由![]() ,可得
,可得![]() ,
,
又![]() 在
在![]() 单调递减,故当
单调递减,故当![]() 时,
时,![]() ,
,
从而![]() ,解得
,解得![]() ,
,
综上,故实数![]() 的最大值为
的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某校“凌云杯”篮球队的成员来自学校高一、高二共10个班的12位同学,其中高一(3)班、高二(3)各出2人,其余班级各出1人,这12人中要选6人为主力队员,则这6人来自不同的班级的概率为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() ,B为AC的中点,分别以AB,AC为直径在AC的同侧作半圆,M,N分别为两半圆上的动点
,B为AC的中点,分别以AB,AC为直径在AC的同侧作半圆,M,N分别为两半圆上的动点![]() 不含端点A,B,
不含端点A,B,![]() ,且
,且![]() ,则
,则![]() 的最大值为______.
的最大值为______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知变量![]() 、
、![]() 之间的线性回归方程为
之间的线性回归方程为![]() ,且变量
,且变量![]() 、
、![]() 之间的一-组相关数据如下表所示,则下列说法错误的是( )
之间的一-组相关数据如下表所示,则下列说法错误的是( )
|
|
|
|
|
|
|
|
|
|
A.可以预测,当![]() 时,
时,![]() B.
B.![]()
C.变量![]()
![]() 之间呈负相关关系D.该回归直线必过点
之间呈负相关关系D.该回归直线必过点![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,记A1F与平面BCC1B1所成的角为θ,下列说法正确的个数是( )
①点F的轨迹是一条线段
②A1F与D1E不可能平行
③A1F与BE是异面直线
④![]()
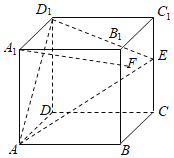
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某人工景观湖外围有两条相互垂直的直线型公路ll,l2,且ll和l2交于点O.为了方便游客游览,计划修建一条连接公路与景观湖的直线型公路AB.景观湖的轮廓可以近似看成一个圆心为O,半径为2百米的圆,且公路AB与圆O相切,圆心O到ll,l2的距离均为5百米,设OAB=![]() ,AB长为L百米.
,AB长为L百米.
(1)求L关于![]() 的函数解析式;
的函数解析式;
(2)当![]() 为何值时,公路AB的长度最短?
为何值时,公路AB的长度最短?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在![]() 上的单调函数,且对任意的x∈
上的单调函数,且对任意的x∈![]() 都有
都有![]() ,则方程
,则方程![]() 的一个根所在的区间是( )
的一个根所在的区间是( )
A. (0,1) B. (1,2) C. (2,3) D. (3,4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生从全校学生中随机选取![]() 名统计他们的鞋码大小,得到如下数据:
名统计他们的鞋码大小,得到如下数据:
鞋码 |
|
|
|
|
|
|
|
|
|
| 合计 |
男生 |
|
|
|
|
|
|
|
|
| ||
女生 |
|
|
|
|
|
|
|
|
|
以各性别各鞋码出现的频率为概率.
(![]() )从该校随机挑选一名学生,求他(她)的鞋码为奇数的概率.
)从该校随机挑选一名学生,求他(她)的鞋码为奇数的概率.
(![]() )为了解该校学生考试作弊的情况,从该校随机挑选
)为了解该校学生考试作弊的情况,从该校随机挑选![]() 名学生进行抽样调查.每位学生从装有除颜色外无差别的
名学生进行抽样调查.每位学生从装有除颜色外无差别的![]() 个红球和
个红球和![]() 个白球的口袋中,随机摸出两个球,若同色,则如实回答其鞋码是否为奇数;若不同色,则如实回答是否曾在考试中作弊.这里的回答,是指在纸上写下“是”或“否”.若调查人员回收到
个白球的口袋中,随机摸出两个球,若同色,则如实回答其鞋码是否为奇数;若不同色,则如实回答是否曾在考试中作弊.这里的回答,是指在纸上写下“是”或“否”.若调查人员回收到![]() 张“是”的小纸条,试估计该校学生在考试中曾有作弊行为的概率.
张“是”的小纸条,试估计该校学生在考试中曾有作弊行为的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com