
【题目】已知函数f(x)=cosx(x∈(0,2π))有两个不同的零点x1、x2 , 方程f(x)=m有两个不同的实根x3、x4 . 若把这四个数按从小到大排列构成等差数列,则实数m的值为( )
A.![]()
B.![]()
C.![]()
D.- ![]()
【答案】D
【解析】解:由题意可知:x1= ![]() ,x2=
,x2= ![]() ,且x3、x4只能分布在x1、x2的中间或两侧,若x3、x4只能分布在x1、x2的中间,则公差d=
,且x3、x4只能分布在x1、x2的中间或两侧,若x3、x4只能分布在x1、x2的中间,则公差d= ![]() =
= ![]() ,
,
故x3、x4分别为 ![]() 、
、 ![]() ,此时可求得m=cos
,此时可求得m=cos ![]() =﹣
=﹣ ![]() ;
;
若x3、x4只能分布在x1、x2的两侧,则公差d= ![]() =π,
=π,
故x3、x4分别为 ![]() 、
、 ![]() ,不合题意.
,不合题意.
故选D
【考点精析】本题主要考查了等差数列的性质和函数的零点的相关知识点,需要掌握在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列;函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点才能正确解答此题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在正三棱柱ABCA1B1C1中,AB=2,AA1=2,由顶点B沿棱柱侧面(经过棱AA1)到达顶点C1,与AA1的交点记为M.求:
(1)三棱柱侧面展开图的对角线长;
(2)从B经M到C1的最短路线长及此时![]() 的值.
的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,角A,B,C的对边分别为a,b,c,a=b(sinC+cosC).
(Ⅰ)求∠ABC;
(Ⅱ)若∠A= ![]() ,D为△ABC外一点,DB=2,DC=1,求四边形ABDC面积的最大值.
,D为△ABC外一点,DB=2,DC=1,求四边形ABDC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人进行围棋比赛,约定每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或打满8局时停止.设甲在每局中获胜的概率为![]() ,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为![]() .
.
(1)求![]() 的值;
的值;
(2)设![]() 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,且f(x)=x有唯一解,
,且f(x)=x有唯一解,![]() ,xn+1=f(xn)(n∈N*).
,xn+1=f(xn)(n∈N*).
(1)求实数a的值;
(2)求数列{xn}的通项公式;
(3)若![]() ,数列b1,b2-b1,b3-b2,…,bn-bn-1是首项为1,公比为
,数列b1,b2-b1,b3-b2,…,bn-bn-1是首项为1,公比为![]() 的等比数列,记cn=anbn,求数列{cn}的前n项和Sn.
的等比数列,记cn=anbn,求数列{cn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面有五个命题:
①函数y=sin4x-cos4x的最小正周期是![]() ;
;
②终边在y轴上的角的集合是{α|α=![]() ;
;
③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点;
④把函数![]() ;
;
⑤函数![]() 。
。
其中真命题的序号是__________(写出所有真命题的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设斜率为2的直线l,过双曲线![]() 的右焦 点,且与双曲线的左、右两支分别相交,则双曲线离心率,e的取值范围是 ( )
的右焦 点,且与双曲线的左、右两支分别相交,则双曲线离心率,e的取值范围是 ( )
A. e>![]() B. e>
B. e>![]() C. 1<e<
C. 1<e<![]() D. 1<e<
D. 1<e<![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
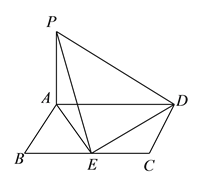
【题目】(本小题满分![]() 分)
分)
如图,平行四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,点
,点![]() 为
为![]() 中点,连结
中点,连结![]() 、
、![]() .
.
(Ⅰ)若![]() ,
, ![]() ,求证:平面
,求证:平面![]() 平面
平面![]() .
.
(Ⅱ)若![]() ,试探究在直线
,试探究在直线![]() 上有几个点
上有几个点![]() ,使得
,使得![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com