




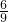 =
= ;
;

 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:044
以下各对应中,哪些是从集合A到集合B的映射?其中哪些是A到B上的一一映射?试说明理由.
(1) A = R, B = R,对应法则f :取倒数;
(2) A ={平面M内的圆},B ={平面M内的点},f :取A中圆的圆心;
(3) A ={平面M内的点},B ={平面M内的圆},f :取A中的点为圆心画圆;
(4) A ={(x,y)![]() y = 2x+1},B ={(x,y)
y = 2x+1},B ={(x,y)![]() y = 2x},f :右移
y = 2x},f :右移![]() 个单位;
个单位;
(5) A ={(x,y)![]() y = 2x+1},B ={(x,y)
y = 2x+1},B ={(x,y)![]() y = 2x},f :下移1个单位;
y = 2x},f :下移1个单位;
(6) A=N, B=N,f :乘以2.
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
(1) A = R, B = R,对应法则f :取倒数;
(2) A ={平面M内的圆},B ={平面M内的点},f :取A中圆的圆心;
(3) A ={平面M内的点},B ={平面M内的圆},f :取A中的点为圆心画圆;
(4) A ={(x,y)![]() y = 2x+1},B ={(x,y)
y = 2x+1},B ={(x,y)![]() y = 2x},f :右移
y = 2x},f :右移![]() 个单位;
个单位;
(5) A ={(x,y)![]() y = 2x+1},B ={(x,y)
y = 2x+1},B ={(x,y)![]() y = 2x},f :下移1个单位;
y = 2x},f :下移1个单位;
(6) A=N, B=N,f :乘以2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com