
 如图|$\overrightarrow{OA}|=|\overrightarrow{OB}$|=1,$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OC}$与$\overrightarrow{OA}$的夹角为30°,|$\overrightarrow{OC}$|=5,则$\overrightarrow{OC}$=$\frac{10\sqrt{3}}{3}$$\overrightarrow{OA}$+$\frac{5\sqrt{3}}{3}$$\overrightarrow{OB}$.(用$\overrightarrow{OA}和\overrightarrow{OB}$表示)
如图|$\overrightarrow{OA}|=|\overrightarrow{OB}$|=1,$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OC}$与$\overrightarrow{OA}$的夹角为30°,|$\overrightarrow{OC}$|=5,则$\overrightarrow{OC}$=$\frac{10\sqrt{3}}{3}$$\overrightarrow{OA}$+$\frac{5\sqrt{3}}{3}$$\overrightarrow{OB}$.(用$\overrightarrow{OA}和\overrightarrow{OB}$表示) 分析 以O为直角坐标原点,OA所在直线为x轴,建立直角坐标系求得A,B,C的坐标,设$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$,利用向量坐标运算、向量基本定理解方程即可得出.
解答 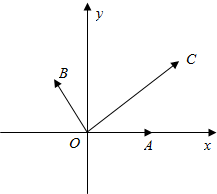 解:如图所示,建立直角坐标系.
解:如图所示,建立直角坐标系.
由$\overrightarrow{OC}$与$\overrightarrow{OA}$的夹角为30°,|$\overrightarrow{OC}$|=5,可得C($\frac{5\sqrt{3}}{2}$,$\frac{5}{2}$),
|$\overrightarrow{OA}|=|\overrightarrow{OB}$|=1,$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,
可得B(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),A(1,0),
设$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$,
则($\frac{5\sqrt{3}}{2}$,$\frac{5}{2}$)=m(1,0)+n(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$)
∴$\frac{5\sqrt{3}}{2}$=m-$\frac{1}{2}$n,$\frac{5}{2}$=$\frac{\sqrt{3}}{2}$n.
解得n=$\frac{5\sqrt{3}}{3}$,m=$\frac{10\sqrt{3}}{3}$.
∴$\overrightarrow{OC}$=$\frac{10\sqrt{3}}{3}$$\overrightarrow{OA}$+$\frac{5\sqrt{3}}{3}$$\overrightarrow{OB}$.
故答案为:$\frac{10\sqrt{3}}{3}$$\overrightarrow{OA}$+$\frac{5\sqrt{3}}{3}$$\overrightarrow{OB}$.
点评 本题考查了向量坐标运算、向量基本定理,考查了计算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | R | B. | [0,2]∪{3} | C. | [0,+∞) | D. | [-3,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
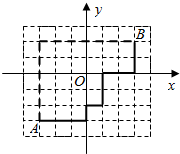 现代城市大多是棋盘式布局(如上海道路几乎都是东西和南北走向).在这样的城市中,我们说的两点间的距离往往不是指两点间的直线距离(位移),而是实际路程(如图).在直角坐标平面内,我们定义A(x1,y1)、B(x2,y2)两点间的“直角距离”为:D(AB)=|x1-x2|+|y1-y2|.
现代城市大多是棋盘式布局(如上海道路几乎都是东西和南北走向).在这样的城市中,我们说的两点间的距离往往不是指两点间的直线距离(位移),而是实际路程(如图).在直角坐标平面内,我们定义A(x1,y1)、B(x2,y2)两点间的“直角距离”为:D(AB)=|x1-x2|+|y1-y2|.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{9}$ | B. | -$\frac{5}{6}$ | C. | -$\frac{7}{18}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com