
【题目】如图所示,等腰![]() 的底边
的底边![]() ,高
,高![]() ,点
,点![]() 是线段
是线段![]() 上异于点
上异于点![]() 的动点,点
的动点,点![]() 在
在![]() 边上,且
边上,且![]() ,现沿
,现沿![]() 将△
将△![]() 折起到△
折起到△![]() 的位置,使
的位置,使![]() ,记
,记![]() ,
, ![]() 表示四棱锥
表示四棱锥![]() 的体积.
的体积.
(1)求![]() 的表达式;(2)当
的表达式;(2)当![]() 为何值时,
为何值时, ![]() 取得最大,并求最大值。
取得最大,并求最大值。
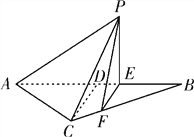
【答案】(1) VP-ACFE=![]() (2)
(2) ![]()
![]()
【解析】试题分析:(1)![]() ,S四边形ACFE=S△ABC-S△BEF=
,S四边形ACFE=S△ABC-S△BEF=![]() ,所以四棱锥P-ACFE的体积VP-ACFE=
,所以四棱锥P-ACFE的体积VP-ACFE=![]() S四边形ACFE·PE=
S四边形ACFE·PE=![]() ;(2)V′(x)=0
;(2)V′(x)=0 ![]() ,所以
,所以![]()
![]() 。
。
试题解析:
(1)因为EF⊥AB,所以EF⊥PE.又因为PE⊥AE,EF∩AE=E,所以PE⊥平面ACFE. 因为EF⊥AB,CD⊥AB,且CD,EF共面,所以EF∥CD,
所以![]()
![]()
所以四边形ACFE的面积
S四边形ACFE=S△ABC-S△BEF=![]()
所以四棱锥P-ACFE的体积VP-ACFE=![]() S四边形ACFE·PE=
S四边形ACFE·PE=![]()
(2)由(1)知. ![]() 令V′(x)=0
令V′(x)=0 ![]() 因为当
因为当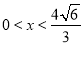 时,V′(x)>0, 当
时,V′(x)>0, 当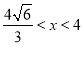 时,V′(x)<0.所以当
时,V′(x)<0.所以当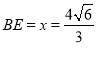 时,
时, 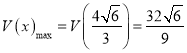


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 被直线
被直线![]() ,
, ![]() 分成面积相等的四个部分,且截
分成面积相等的四个部分,且截![]() 轴所得线段的长为2.
轴所得线段的长为2.
(1)求![]() 的方程;
的方程;
(2)若存在过点![]() 的直线与
的直线与![]() 相交于
相交于![]() ,
, ![]() 两点,且点
两点,且点![]() 恰好是线段
恰好是线段![]() 的中点,求实数
的中点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家电公司销售部门共有200位销售员,每位部门对每位销售员都有1400万元的年度销售任务,已知这200位销售员去年完成销售额都在区间![]() (单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为
(单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,绘制出频率分布直方图.
,绘制出频率分布直方图.

(1)求![]() 的值,并计算完成年度任务的人数;
的值,并计算完成年度任务的人数;
(2)用分层抽样从这200位销售员中抽取容量为25的样本,求这5组分别应抽取的人数;
(3)现从(2)中完成年度任务的销售员中随机选取2位,奖励海南三亚三日游,求获得此奖励的2位销售员在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若函数![]() 在区间[0,1]上存在零点,求实数
在区间[0,1]上存在零点,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,若对任意
时,若对任意![]() ∈[0,4],总存在
∈[0,4],总存在![]() ∈[0,4],使
∈[0,4],使![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《算法统宗》是中国古代数学名著,由明代数学家程大位编著. 《算法统宗》对我国民间普及珠算和数学知识起到了很大的作用,是东方古代数学的名著.在这部著作中,许多数学问题都是以歌诀形式呈现的,以“竹筒容米”就是其中一首:家有九节竹一茎,为因盛米不均平;下头三节三升九,上梢四节贮三升;唯有中间二节竹,要将米数次第盛;若是先生能算法,也教算得到天明!大意是:用一根9节长的竹子盛米,每节竹筒盛米的容积是不均匀的.下端3节可盛米3.9升,上端4节可盛米3升,要按每节依次盛容积相差同一数量的方式盛米,中间两节可盛米多少升?由以上条件,计算出中间两节的容积为( )
A. ![]() 升 B.
升 B. ![]() 升 C.
升 C. ![]() 升 D.
升 D. ![]() 升
升
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】光线从点A(-3,4)射出,到x轴上的点B后,被x轴反射到y轴上的点C,又被y轴反射,这时反射光线恰好过点D(-1,6),求光线BC所在直线的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com