
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线为
处的切线为![]() ,若
,若![]() 时,
时,![]() 有极值.
有极值.
(1)求![]() 的值;
的值;
(2)求![]() 在
在![]() 上的最大值和最小值.
上的最大值和最小值.
【答案】解: (1)由f(x)=x3+ax2+bx+c,
得f′(x)=3x2+2ax+b,
当x=1时,切线l的斜率为3,可得2a+b="0 " ①
当x=![]() 时,y=f(x)有极值,则f′(
时,y=f(x)有极值,则f′(![]() )=0,
)=0,
可得4a+3b+4="0 " ②
由①②解得a=2,b=-4.
由于切点的横坐标为x=1,∴f(1)=4.
∴1+a+b+c=4.∴c=5………………………………….6分
(2)由(1)可得f(x)=x3+2x2-4x+5,
∴f′(x)=3x2+4x-4,
令f′(x)=0,得x=-2,x=![]() .
.
当x变化时,y,y′的取值及变化如下表:
x | -3 | (-3,-2) | -2 | (-2, |
| ( | 1 |
| + | 0 | - | 0 | + | ||
y | 8 |
| 13 |
|
|
| 4 |
∴ y=f(x)在[-3,1]上的最大值为13,最小值为![]() …………………….14分
…………………….14分
【解析】试题分析:
(1)利用题意求得实数a,b,c的值可得函数f(x)的表达式为f(x)=x3+2x2-4x+5
(2)结合(1)的解析式和导函数研究原函数的性质可得y=f(x)在[-3,1]上的最大值为13,最小值为![]() .
.
试题解析:
(1)由f(x)=x3+ax2+bx+c,
得f′(x)=3x2+2ax+b,
当x=1时,切线l的斜率为3,可得2a+b=0;①
当x=![]() 时,y=f(x)有极值,则f′
时,y=f(x)有极值,则f′![]() =0,
=0,
可得4a+3b+4=0.②
由①②解得a=2,b=-4,
又切点的横坐标为x=1,∴f(1)=4.
∴1+a+b+c=4.∴c=5.
(2)由(1),得f(x)=x3+2x2-4x+5,
∴f′(x)=3x2+4x-4.
令f′(x)=0,得x=-2或x=![]() ,
,
∴f′(x)<0的解集为![]() ,即为f(x)的减区间.
,即为f(x)的减区间.
[-3,-2)、![]() 是函数的增区间.
是函数的增区间.
又f(-3)=8,f(-2)=13,f![]() =
=![]() ,f(1)=4,
,f(1)=4,
∴y=f(x)在[-3,1]上的最大值为13,最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)证明:函数![]() 是偶函数;
是偶函数;
(2)利用绝对值及分段函数知识,将函数解析式写成分段函数的形式,然后画出函数图像(草图),并写出函数的值域;
(3)在同一坐标系中画出直线![]() ,观察图像写出不等式
,观察图像写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
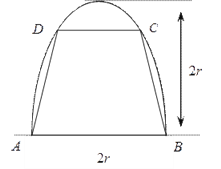
【题目】如图,有一块半椭圆形钢板,其长半轴为![]() ,短半轴为
,短半轴为![]() ,计划将此钢板切割成等腰梯形的形状,下底
,计划将此钢板切割成等腰梯形的形状,下底![]() 是半椭圆的短轴,上底
是半椭圆的短轴,上底![]() 的端点在椭圆上,记
的端点在椭圆上,记![]() ,梯形面积为
,梯形面积为![]() .
.
(Ⅰ)求面积![]() 关于变量
关于变量![]() 的函数表达式,并写出定义域;
的函数表达式,并写出定义域;
(Ⅱ)求面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:指数函数f(x)=(2a-6)x在R上是单调减函数;q:关于x的方程x2-3ax+2a2+1=0的两根均大于3,若p或q为真,p且q为假,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用长为18 m的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题,其中正确的序号是__________________(写出所有正确命题的序号)
①函数![]() 的图像恒过定点
的图像恒过定点![]() ;
;
②已知集合![]() ,则映射
,则映射![]() 中满足
中满足![]() 的映射共有1个;
的映射共有1个;
③若函数![]() 的值域为R,则实数
的值域为R,则实数![]() 的取值范围是
的取值范围是![]() ;
;
④函数![]() 的图像关于
的图像关于![]() 对称的函数解析式为
对称的函数解析式为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x-1|+|x+1|(x∈R).
(1)证明:函数f(x)是偶函数;
(2)利用绝对值及分段函数知识,将函数解析式写成分段函数的形式,然后画出函数图象;
(3)写出函数的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com