【题目】如图是国家统计局公布的2013-2018年入境游客（单位：万人次）的变化情况，则下列结论错误的是（ ）
A.2014年我国入境游客万人次最少
B.后4年我国入境游客万人次呈逐渐增加趋势
C.这6年我国入境游客万人次的中位数大于13340万人次
D.前3年我国入境游客万人次数据的方差小于后3年我国入境游客万人次数据的方差
科目：高中数学 来源： 题型：
【题目】某搜索引擎广告按照付费价格对搜索结果进行排名，点击一次付费价格排名越靠前，被点击的次数也可能会提高，已知某关键词被甲、乙等多个公司竞争，其中甲、乙付费情况与每小时点击量结果绘制成如下的折线图.
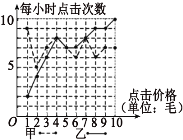
（1）若甲公司计划从这10次竞价中随机抽取3次竞价进行调研，其中每小时点击次数超过7次的竞价抽取次数记为
，求的分布列与数学期望；
（2）若把乙公司设置的每次点击价格为x，每小时点击次数为
，则点
近似在一条直线附近.试根据前5次价格与每小时点击次数的关系，求y关于x的回归直线
.（附：回归方程系数公式：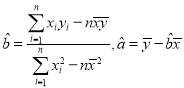
）.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于函数
的定义域为
，如果存在区间
，同时满足下列条件：
①
在
上是单调函数；
②当的定义域为时，值域也是，则称区间是函数的“
区间”.对于函数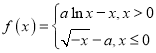
.
（1）若
，求函数在
处的切线方程；
（2）若函数在
上存在“区间”，求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知底面为边长为
的正方形，侧棱长为
的直四棱柱
中，
是上底面
上的动点.给出以下四个结论中，正确的个数是（ ）
①与点
距离为
的点形成一条曲线，则该曲线的长度是
；
②若
面
，则
与面
所成角的正切值取值范围是
；
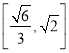③若
，则在该四棱柱六个面上的正投影长度之和的最大值为
.
A.
B.C.D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】以下命题：（1）已知三个不同的平面
，
，
，若
，
，则
；（2）若直线
，
与平面所成角都是
，则这两条直线平行；（3）若直线，与平面所成角都是，则这两条直线不可能垂直；（4）设直线
与平面相交但不垂直，则在平面内有且只有一条直线与直线垂直.错误的个数是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线
过点
，该抛物线的准线与椭圆
:
相切，且椭圆的离心率为
，点
为椭圆的右焦点.
（1）求椭圆的标准方程；
（2）过点的直线
与椭圆交于
两点，
为平面上一定点，且满足
，求直线的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某商场举行优惠促销活动，顾客仅可以从以下两种优惠方案中选择一种.
方案一：每满100元减20元；
方案二：满100元可抽奖一次.具体规则是从装有2个红球、2个白球的箱子随机取出3个球（逐个有放回地抽取），所得结果和享受的优惠如下表：（注：所有小球仅颜色有区别）
红球个数 | 3 | 2 | 1 | 0 |
实际付款 | 7折 | 8折 | 9折 | 原价 |
（1）该商场某顾客购物金额超过100元，若该顾客选择方案二，求该顾客获得7折或8折优惠的概率；
（2）若某顾客购物金额为180元，选择哪种方案更划算？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
