
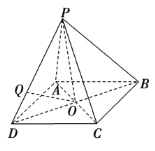
【题目】一个四棱锥的三视图如图所示.

(1)求证:PA⊥BD;
(2)在线段PD上是否存在一点Q,使二面角Q-AC-D的平面角为30°?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)详见解析(2)![]() =
=![]() .
.
【解析】
试题分析:(1)由三视图,可知四棱锥的底面是正方形,侧面是全等的等腰三角形,所以该四棱锥是一个正四棱锥.作出它的直观图,根据线面垂直的判定与性质,可证出PA⊥BD;(2)假设存在点Q,使二面角Q-AC-D的平面角为30°,由AC⊥平面PBD可得∠DOQ为二面角Q-AC-D的平面角,可证出在Rt△PDO中,OQ⊥PD,且∠PDO=60°,结合三角函数的计算可得![]() =
=![]() .
.
试题解析:(1)由三视图可知P-ABCD为四棱锥,底面ABCD为正方形,且PA=PB=PC=PD,连接AC、BD交于点O,连接PO.
因为BD⊥AC,BD⊥PO,所以BD⊥平面PAC,
即BD⊥PA.
(2)由三视图可知,BC=2,PA=2![]() ,假设存在这样的点Q,因为AC⊥OQ,AC⊥OD,
,假设存在这样的点Q,因为AC⊥OQ,AC⊥OD,
所以∠DOQ为二面角Q-AC-D的平面角,
在△POD中,PD=2![]() , OD=
, OD=![]() ,则∠PDO=60°,
,则∠PDO=60°,
在△DQO中,∠PDO=60°,且∠QOD=30°.
所以DP⊥OQ.所以OD=![]() ,QD=
,QD=![]() .
.
所以![]() =
=![]() .
.


科目:高中数学 来源: 题型:
【题目】以下程序运行后的输出结果为
i=1
WHILE i<8
i=i+2
S=2*i+3
i=i–1
WEND
PRINT S
END
A. 17 B. 19 C. 21 D. 23
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于程序框图的说法正确的是( )
①程序框图只有一个入口,也只有一个出口;
②程序框图的第一部分应有一条从入口到出口的路径通过它;
③程序框图的循环可以是无尽循环;
④程序框图中判断框内的条件是唯一的.
A. ①②③ B. ②③ C. ①④ D. ①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,过原点的直线
,过原点的直线![]() 与其交于不同的两点
与其交于不同的两点![]() .
.
(1)求直线![]() 斜率
斜率![]() 的取值范围;
的取值范围;
(2)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)若直线![]() 与曲线
与曲线![]() 只有一个公共点,求
只有一个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将全班同学按学号编号,制作相应的卡片号签,放入同一个箱子里均匀搅拌,从中抽出15个号签,就相应的15名学生对看足球比赛的喜爱程度(很喜爱、喜爱、一般、不喜爱、很不喜爱)进行调查,使用的是___法.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com