Question

【题目】如图，在三棱锥P﹣ABC中，PA⊥底面ABC，∠BAC=90°．点D，E，N分别为棱PA，PC，BC的中点，M是线段AD的中点，PA=AC=4，AB=2．

（Ⅰ）求证：MN∥平面BDE；
（Ⅱ）求二面角C﹣EM﹣N的正弦值；
（Ⅲ）已知点H在棱PA上，且直线NH与直线BE所成角的余弦值为 ，求线段AH的长．

Answer 1

【答案】（Ⅰ）证明：取AB中点F，连接MF、NF，

∵M为AD中点，∴MF∥BD，
∵BD平面BDE，MF平面BDE，∴MF∥平面BDE．
∵N为BC中点，∴NF∥AC，
又D、E分别为AP、PC的中点，∴DE∥AC，则NF∥DE．
∵DE平面BDE，NF平面BDE，∴NF∥平面BDE．
又MF∩NF=F．
∴平面MFN∥平面BDE，则MN∥平面BDE；
（Ⅱ）解：∵PA⊥底面ABC，∠BAC=90°．
∴以A为原点，分别以AB、AC、AP所在直线为x、y、z轴建立空间直角坐标系．
∵PA=AC=4，AB=2，
∴A（0，0，0），B（2，0，0），C（0，4，0），M（0，0，1），N（1，2，0），E（0，2，2），
则 ， ，
设平面MEN的一个法向量为 ，
由 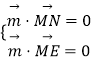，得 ，取z=2，得 ．
由图可得平面CME的一个法向量为 ．
∴cos＜ ＞= ．
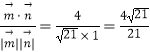∴二面角C﹣EM﹣N的余弦值为 ，则正弦值为 ；
（Ⅲ）解：设AH=t，则H（0，0，t）， ， ．
∵直线NH与直线BE所成角的余弦值为 ，
∴|cos＜ ＞|=| |=| |= ．
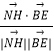解得：t=4．
∴当H与P重合时直线NH与直线BE所成角的余弦值为 ，此时线段AH的长为4．
【解析】（Ⅰ）取AB中点F，连接MF、NF，由已知可证MF∥平面BDE，NF∥平面BDE．得到平面MFN∥平面BDE，则MN∥平面BDE；
（Ⅱ）由PA⊥底面ABC，∠BAC=90°．可以A为原点，分别以AB、AC、AP所在直线为x、y、z轴建立空间直角坐标系．求出平面MEN与平面CME的一个法向量，由两法向量所成角的余弦值得二面角C﹣EM﹣N的余弦值，进一步求得正弦值；
（Ⅲ）设AH=t，则H（0，0，t），求出 的坐标，结合直线NH与直线BE所成角的余弦值为 列式求得线段AH的长．
【考点精析】解答此题的关键在于理解异面直线及其所成的角的相关知识，掌握异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系，以及对平面与平面平行的判定的理解，了解判断两平面平行的方法有三种:用定义；判定定理；垂直于同一条直线的两个平面平行．