
【题目】已知![]() ,
, ![]() 分别为等差数列和等比数列,
分别为等差数列和等比数列, ![]() ,
, ![]() 的前
的前![]() 项和为
项和为![]() .函数
.函数![]() 的导函数是
的导函数是![]() ,有
,有![]() ,且
,且![]() 是函数
是函数![]() 的零点.
的零点.
(1)求![]() 的值;
的值;
(2)若数列![]() 公差为
公差为![]() ,且点
,且点![]() ,当
,当![]() 时所有点都在指数函数
时所有点都在指数函数![]() 的图象上.
的图象上.
请你求出![]() 解析式,并证明:
解析式,并证明: ![]() .
.
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈[1,12],x2﹣a≥0.命题q:x0∈R,使得x02+(a﹣1)x0+1<0.若p或q为真,p且q为假,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() ,
, ![]() 分别是
分别是![]() 中点,弧
中点,弧![]() 的半径分别为
的半径分别为![]() ,点
,点![]() 平分弧
平分弧![]() ,过点
,过点![]() 作弧
作弧![]() 的切线分别交
的切线分别交![]() 于点
于点![]() .四边形
.四边形![]() 为矩形,其中点
为矩形,其中点![]() 在线段
在线段![]() 上,点
上,点![]() 在弧
在弧![]() 上,延长
上,延长![]() 与
与![]() 交于点
交于点![]() .设
.设![]() ,矩形
,矩形![]() 的面积为
的面积为![]() .
.
(1)求![]() 的解析式并求其定义域;
的解析式并求其定义域;
(2)求![]() 的最大值.
的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过原点的动直线l与圆C1:x2+y2﹣6x+5=0相交于不同的两点A,B.
(1)求圆C1的圆心坐标;
(2)求线段AB 的中点M的轨迹C的方程;
(3)是否存在实数 k,使得直线L:y=k(x﹣4)与曲线 C只有一个交点?若存在,求出k的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二(1)班学生为了筹措经费给班上购买课外读物,班委会成立了一个社会实践小组,决定利用暑假八月份(30天计算)轮流换班去销售一种时令水果.在这30天内每斤水果的收入![]() (元)与时间
(元)与时间![]() (天)的部分数据如下表所示,已知日销售
(天)的部分数据如下表所示,已知日销售![]() (斤)与时间
(斤)与时间![]() (天)满足一次函数关系.
(天)满足一次函数关系.
(1)根据提供的图象和表格,下厨每斤水果的收入![]() (元)与时间
(元)与时间![]() (天)所满足的函数关系式及日销售量
(天)所满足的函数关系式及日销售量![]() (斤)与时间
(斤)与时间![]() (天)的一次函数关系;
(天)的一次函数关系;
(2)用![]() (元)表示销售水果的日收入,写出
(元)表示销售水果的日收入,写出![]() 与
与![]() 的函数关系式,并求这30天中第几天日收入最大,最大值为多少元?
的函数关系式,并求这30天中第几天日收入最大,最大值为多少元?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得 ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a;
(Ⅱ)判断变量x与y之间是正相关还是负相关;
(Ⅲ)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程y=bx+a中, 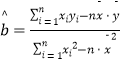 ,
, ![]() ,其中
,其中 ![]() ,
, ![]() 为样本平均值,线性回归方程也可写为
为样本平均值,线性回归方程也可写为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a是实数,f(x)=a﹣ ![]() (x∈R).
(x∈R).
(1)证明不论a为何实数,f(x)均为增函数;
(2)若f(x)满足f(﹣x)+f(x)=0,解关于x的不等式f(x+1)+f(1﹣2x)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,点P在正方形ABCD所在平面外,PA⊥平面ABCD,PA=AB,则PB与AC所成的角是( ) 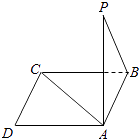
A.90°
B.60°
C.45°
D.30°
查看答案和解析>>
科目:高中数学 来源: 题型:
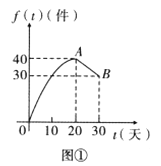
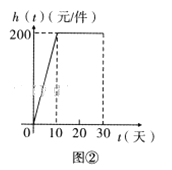
【题目】某公司研发出一款产品,批量生产前先在某城市销售30天进行市场调查.调查结果发现:日销量![]() 与天数
与天数![]() 的对应关系服从图①所示的函数关系:每件产品的销售利润
的对应关系服从图①所示的函数关系:每件产品的销售利润![]() 与天数
与天数![]() 的对应关系服从图②所示的函数关系.图①由抛物线的一部分(
的对应关系服从图②所示的函数关系.图①由抛物线的一部分(![]() 为抛物线顶点)和线段
为抛物线顶点)和线段![]() 组成.
组成.
(Ⅰ)设该产品的日销售利润![]()
![]() ,分别求出
,分别求出![]() ,
, ![]() ,
, ![]() 的解析式,
的解析式,
(Ⅱ)若在30天的销售中,日销售利润至少有一天超过8500元,则可以投入批量生产,该产品是否可以投入批量生产,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com