
【题目】已知函数![]() 的图像在
的图像在![]() 上连续不断,定义:
上连续不断,定义:
![]() (
(![]() ),
),![]() (
(![]() ),其中
),其中![]() 表示函数
表示函数![]() 在
在![]() 上的最小值,
上的最小值, ![]() 表示函数
表示函数![]() 在
在![]() 上的最大值,若存在最小正整数
上的最大值,若存在最小正整数![]() ,使得
,使得![]() 对任意的
对任意的![]() 成立,则称函数
成立,则称函数![]() 为
为![]() 上的“
上的“![]() 阶收缩函数”.
阶收缩函数”.
(1)若![]() ,
, ![]() ,试写出
,试写出![]() ,
, ![]() 的表达式;
的表达式;
(2)已知函数![]() ,
, ![]() ,判断
,判断![]() 是否为
是否为![]() 上的“
上的“![]() 阶收缩函数”,如果是,求出对应的
阶收缩函数”,如果是,求出对应的![]() ,如果不是,请说明理由;
,如果不是,请说明理由;
(3)已知![]() ,函数
,函数![]() ,是
,是![]() 上的2阶收缩函数,求
上的2阶收缩函数,求![]() 的取值范围.
的取值范围.
数学附加题
【答案】(1) ![]() ,
, ![]() ,
, ![]() ,
, ![]() . (2)
. (2) ![]() .即存在
.即存在![]() ,使得
,使得![]() 是
是![]() 上的“4阶收缩函数”. (3)
上的“4阶收缩函数”. (3) ![]()
【解析】试题分析:(1)根据![]() 的最大值可求出
的最大值可求出![]() ,
, ![]() 的解析式;(2)根据函数
的解析式;(2)根据函数![]() ,
, ![]() 上的值域,先求出
上的值域,先求出![]() ,
, ![]() 的解析式,再根据
的解析式,再根据![]() 求出k的取值范围得到答案.(3)先对函数
求出k的取值范围得到答案.(3)先对函数![]() 求导判断函数的单调性,进而写出
求导判断函数的单调性,进而写出![]() ,
, ![]() 的解析式,然后再由
的解析式,然后再由![]() 求出k的取值范围.
求出k的取值范围.
试题解析:
(1)由题意可得: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(2)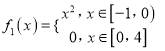 ,
, 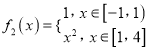 ,
, 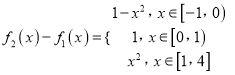
当![]() 时,
时, ![]() ,∴
,∴![]() ,
, ![]() ;
;
当![]() 时,
时, ![]() ,∴
,∴![]() ,∴
,∴![]() ;
;
当![]() 时,
时, ![]() ,∴
,∴![]() ,
, ![]()
综上所述, ![]() .即存在
.即存在![]() ,使得
,使得![]() 是
是![]() 上的“4阶收缩函数”.
上的“4阶收缩函数”.
(3)![]() ,令
,令![]() 得
得![]() 或
或![]() .函数
.函数![]() 的变化情况如下:
的变化情况如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
令![]() 得
得![]() 或
或![]() .
.
(1)当![]() 时,
时, ![]() 在
在![]() 上单调递增,因此,
上单调递增,因此, ![]() ,
, ![]() .因为
.因为![]() 是
是![]() 上的“二阶收缩函数”,所以,
上的“二阶收缩函数”,所以,
①![]() ,对
,对![]() 恒成立;
恒成立;
②存在![]() ,使得
,使得![]() 成立.
成立.
①即: ![]() 对
对![]() 恒成立,由
恒成立,由![]() 解得
解得![]() 或
或![]() .
.
要使![]() 对
对![]() 恒成立,需且只需
恒成立,需且只需![]() .
.
②即:存在![]() ,使得
,使得![]() 成立.
成立.
由![]() 解得
解得![]() 或
或![]() .所以,只需
.所以,只需![]() .
.
综合①②可得![]()
(2)当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,因此,
上单调递减,因此, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,显然当
,显然当![]() 时,
时, ![]() 不成立,
不成立,
(3)当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,因此,
上单调递减,因此, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,显然当
,显然当![]() 时,
时, ![]() 不成立.
不成立.
综合(1)(2)(3)可得: ![]() .
.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 是递增的等比数列,满足
是递增的等比数列,满足![]() ,且
,且![]() 是
是![]() 、
、![]() 的等差中项,数列
的等差中项,数列![]() 满足
满足![]() ,其前
,其前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)数列![]() 的前
的前![]() 项和为
项和为![]() ,若不等式
,若不等式![]() 对一切
对一切![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
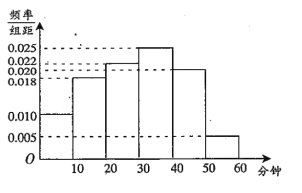
【题目】某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集的数据分成![]() 六组,并作出频率分布直方图(如图),将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
六组,并作出频率分布直方图(如图),将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
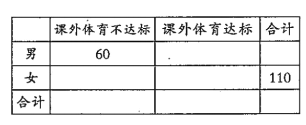
(1)请根据直方图中的数据填写下面的![]() 列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
(2)在[0,10),[40,50)这两组中采取分层抽样,抽取6人,再从这6名学生中随机抽取2人参加体育知识问卷调查,求这2人中一人来自“课外体育达标”和一人来自“课外体育不达标”的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)过点(1,
(a>b>0)过点(1, ![]() ),且离心率e=
),且离心率e=![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l:y=kx+m与椭圆C相交于A,B两点(A,B不是左右顶点),椭圆的右顶点为D,且满足![]() ·
·![]() =0,试判断直线l是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.
=0,试判断直线l是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某广场中间有一块边长为2百米的菱形状绿化区![]() ,其中
,其中![]() 是半径为1百米的扇形,
是半径为1百米的扇形,![]() . 管理部门欲在该地从
. 管理部门欲在该地从![]() 到
到![]() 修建小路:在弧
修建小路:在弧![]() 上选一点
上选一点![]() (异于
(异于![]() 两点),过点
两点),过点![]() 修建与
修建与![]() 平行的小路
平行的小路![]() .问:点
.问:点![]() 选择在何处时,才能使得修建的小路
选择在何处时,才能使得修建的小路![]() 与
与![]() 及
及![]() 的总长最小?并说明理由.
的总长最小?并说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856307)(12分)
某老师为了分析学生的学习情况,随机抽取了班上20名学生某次期末考试的成绩(满分为150分)进行分析,统计如下:
男生:133 131 130 126 123 120 116 109 107 105
女生:136 127 125 123 119 118 117 114 113 108
(Ⅰ)计算男、女生成绩的平均值并分析比较男、女生成绩的分散程度;
(Ⅱ)现从分数在120分以下的女同学中随机抽取2位,求这两位同学分数之差的绝对值小于10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856335)[选修4-4:坐标系与参数方程]
以原点为极点,x轴的非负半轴为极轴建立极坐标系.已知A(2,π),B(2, ![]() ),圆C的极坐标方程为ρ2-6ρcos θ+8ρsin θ+21=0.F为圆C上的任意一点.
),圆C的极坐标方程为ρ2-6ρcos θ+8ρsin θ+21=0.F为圆C上的任意一点.
(Ⅰ)写出圆C的参数方程;
(Ⅱ)求△ABF的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A是函数y=lg(20﹣8x﹣x2)的定义域,集合B是不等式x2﹣2x+1﹣a2≥0(a>0)的解集,p:x∈A,q:x∈B.
(1)若A∩B=,求实数a的取值范围;
(2)若¬p是q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com