
(08年福州质检二文)(12分)
如图,直三棱柱A1B1C1―ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.
(Ⅰ)求![]() 与平面A1C1CA所成角的大小;
与平面A1C1CA所成角的大小;
(Ⅱ)求二面角B―A1D―A的大小;
(Ⅲ)点F是线段AC的中点,证明:EF⊥平面A1BD.

解析:(Ⅰ)连接A1C.∵A1B1C1-ABC为直三棱柱,∴CC1⊥底面ABC,∴CC1⊥BC.
∵AC⊥CB,∴BC⊥平面A1C1CA. ………………1分
∴![]() 为
为![]() 与平面A1C1CA所成角,
与平面A1C1CA所成角,
![]() .
.
∴![]() 与平面A1C1CA所成角为
与平面A1C1CA所成角为![]() .………3分
.………3分
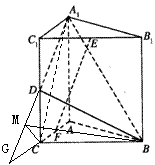
(Ⅱ)分别延长AC,A1D交于G. 过C作CM⊥A1G 于M,连结BM,
∵BC⊥平面ACC1A1,∴CM为BM在平面A1C1CA内的射影,
∴BM⊥A1G,∴∠CMB为二面角B―A1D―A的平面角,………………………5分
平面A1C1CA中,C1C=CA=2,D为C1C的中点,
∴CG=2,DC=1 在直角三角形CDG中,![]() ,
,![]() .……7分
.……7分
即二面角B―A1D―A的大小为![]() .……………………8分
.……………………8分
(Ⅲ)证明:∵A1B1C1―ABC为直三棱柱,∴B1C1//BC,
∵由(Ⅰ)BC⊥平面A1C1CA,∴B1C1⊥平面A1C1CA,
∵EF在平面A1C1CA内的射影为C1F,∵F为AC中点,
∴C1F⊥A1D,∴EF⊥A1D.……………………11分
同理可证EF⊥BD,∴EF⊥平面A1BD.……………………12分
解法二:
(Ⅰ)同解法一……………………3分
(Ⅱ)∵A1B1C1―ABC为直三棱柱,C1C=CB=CA=2,
AC⊥CB,D、E分别为C1C、B1C1的中点.
建立如图所示的坐标系得:

C(0,0,0),B(2,0,0),A(0,2,0),
C1(0,0,2), B1(2,0,2), A1(0,2,2),
D(0,0,1), E(1,0,2).………………6分
![]() ,设平面A1BD的法向量为
,设平面A1BD的法向量为![]()
![]() ,
,
![]()
![]() .…………6分
.…………6分
平面ACC1A1的法向量为![]() =(1,0,0),
=(1,0,0),![]() .………7分
.………7分
即二面角B―A1D―A的大小为![]() .…………………8分
.…………………8分
(Ⅲ)证明:∵F为AC的中点,∴F(0,1,0),![]() .……10分
.……10分
由(Ⅱ)知平面A1BD的一个法向量为![]() ,∴
,∴![]() //n . ……11分
//n . ……11分
EF⊥平面A1BD.…………………………………12分


科目:高中数学 来源: 题型:
(08年福州质检二文)(12分)
三个人进行某项射击活动,在一次射击中甲、乙、丙三人射中目标的概率分别为![]() 、
、![]() 、
、![]() .
.
(Ⅰ)一次射击后,三人都射中目标的概率是多少?
(Ⅱ)用随机变量![]() 表示三个人在一次射击后射中目标的次数与没有射中目标的次数之差的绝对值.求证
表示三个人在一次射击后射中目标的次数与没有射中目标的次数之差的绝对值.求证![]() 的取值为1或3,并求
的取值为1或3,并求![]() 时的概率.
时的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com