
| A. | 39 | B. | 45 | C. | 50 | D. | 55 |
分析 推导出{$\sqrt{{a}_{n}+1}$}是首项为1,公差为1的等差数列,从而${a}_{n}={n}^{2}-1$,由此能求出a5+S4的值.
解答 解:∵数列{an}的前n和为Sn,a1=0,an+1=an+2$\sqrt{{a}_{n}+1}$+1,
∴$\sqrt{{a}_{n+1}+1}-\sqrt{{a}_{n}+1}$=1,$\sqrt{{a}_{1}+1}=0$,
∴{$\sqrt{{a}_{n}+1}$}是首项为1,公差为1的等差数列,
∴$\sqrt{{a}_{n}+1}$=1+(n-1)×1=n,
∴${a}_{n}={n}^{2}-1$,
∴${a}_{5}={5}^{2}-1$=24,
${S}_{4}={1}^{2}+{2}^{2}+{3}^{2}+{4}^{2}-4$=26.
∴a5+S4=24+26=50.
故选:C.
点评 本题考查数列的前5项和的求法,是基础题,解题时要认真审题,注意构造法的合理运用.


科目:高中数学 来源: 题型:选择题
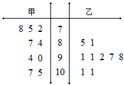 某次运动会甲、乙两名射击运动员成绩如图所示,甲、乙的平均数分别为为 $\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$,方差分别为s甲2,s乙2,则( )
某次运动会甲、乙两名射击运动员成绩如图所示,甲、乙的平均数分别为为 $\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$,方差分别为s甲2,s乙2,则( )| A. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,s甲2>s乙2 | B. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,s甲2<s乙2 | ||
| C. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,s甲2>s乙2 | D. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,s甲2<s乙2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}π{R^2}$ | B. | $\frac{{\sqrt{3}}}{2}π{R^2}$ | C. | πR2 | D. | $\frac{3}{4}π{R^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 2 | C. | 3 | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{72}{13}$ | B. | $\frac{135}{22}$ | C. | $\frac{79}{14}$ | D. | $\frac{142}{23}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2$\sqrt{3}$] | B. | [2,+∞) | C. | (-∞,-2$\sqrt{3}$]∪[2$\sqrt{3}$,+∞) | D. | (-∞,-2$\sqrt{3}$)∪(2$\sqrt{3}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com