
【题目】已知函数![]() .
.
(1)若曲线![]() 在
在![]() 处的切线的斜率为2,求函数
处的切线的斜率为2,求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 在区间
在区间![]() 上有零点,求实数
上有零点,求实数![]() 的取值范围.(
的取值范围.(![]() 是自然对数的底数,
是自然对数的底数,![]() )
)
【答案】(1)函数![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() (2)
(2)![]()
【解析】
(1)求导,由导数的结合意义可求得![]() ,进而得到函数解析式,再解关于导函数的不等式即可得到单调区间;
,进而得到函数解析式,再解关于导函数的不等式即可得到单调区间;
(2)对![]() 进行分类讨论,利用导数,结合零点的存在性定理建立不等式即可求解.
进行分类讨论,利用导数,结合零点的存在性定理建立不等式即可求解.
(1)函数![]() 的定义域为
的定义域为![]() ,
,
![]()
![]() ,
,
则![]() ,所以
,所以![]() ,
,
此时![]() ,定义域为
,定义域为![]() ,
,![]() ,
,
令![]() ,解得
,解得![]() ;令
;令![]() ,解得
,解得![]() ;
;
所以函数![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
(2)函数![]() 在区间
在区间![]() 上的图象是一条不间断的曲线.
上的图象是一条不间断的曲线.
由(1)知![]() ,
,
1)当![]() 时,对任意
时,对任意![]() ,
,![]() ,
,![]() ,则
,则![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上单调递增,此时对任意
上单调递增,此时对任意![]() ,都有
,都有![]() 成立,从而函数
成立,从而函数![]() 在区间
在区间![]() 上无零点;
上无零点;
2)当![]() 时,令
时,令![]() ,得
,得![]() 或
或![]() ,其中
,其中![]() ,
,
①若![]() ,即
,即![]() ,则对任意
,则对任意![]() ,
,![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上单调递减,由题意得
上单调递减,由题意得![]() ,且
,且![]() ,解得
,解得![]() ,其中
,其中![]() ,即
,即![]() ,
,
所以![]() 的取值范围是
的取值范围是![]() ;
;
②若![]() ,即
,即![]() ,则对任意
,则对任意![]() ,
,![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上单调递增,此时对任意
上单调递增,此时对任意![]() ,都有
,都有![]() 成立,从而函数
成立,从而函数![]() 在区间
在区间![]() 上无零点;
上无零点;
③若![]() ,即
,即![]() ,则对任意
,则对任意![]() ,
,![]() ;所以函数
;所以函数![]() 在区间
在区间![]() 上单调递增,对任意
上单调递增,对任意![]() ,都有
,都有![]() 成立;
成立;
对任意![]() ,
,![]() ,函数
,函数![]() 在区间
在区间![]() 上单调递减,由题意得
上单调递减,由题意得
![]() ,解得
,解得![]() ,
,
其中![]() ,即
,即![]() ,
,
所以![]() 的取值范围是
的取值范围是![]() .
.
综上可得,实数![]() 的取值范围是
的取值范围是![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=mx-lnx-1(m为常数).
(1)若函数f(x)恰有1个零点,求实数m的取值范围;
(2)若不等式mx-ex≤f(x)+a对正数x恒成立,求实数a的最小整数值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设s,t是不相等的两个正数,且s+slnt=t+tlns,则s+t﹣st的取值范围为( )
A.(﹣∞,1)B.(﹣∞,0)C.(0,+∞)D.(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,若椭圆经过点
,若椭圆经过点![]() ,且△PF1F2的面积为2.
,且△PF1F2的面积为2.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设斜率为1的直线![]() 与以原点为圆心,半径为
与以原点为圆心,半径为![]() 的圆交于A,B两点,与椭圆C交于C,D两点,且
的圆交于A,B两点,与椭圆C交于C,D两点,且![]() (
(![]() ),当
),当![]() 取得最小值时,求直线
取得最小值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() ,过焦点
,过焦点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() ,
,![]() 两点,且当直线
两点,且当直线![]() 倾斜角为
倾斜角为![]() 时,与抛物线相交所得弦的长度为8.
时,与抛物线相交所得弦的长度为8.
(1)求抛物线![]() 的方程;
的方程;
(2)若分别过点![]() ,
,![]() 两点作抛物线
两点作抛物线![]() 的切线
的切线![]() ,
,![]() ,两条切线相交于点
,两条切线相交于点![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,判断四边形
,判断四边形![]() 是否存在外接圆,如果存在,求出外接圆面积的最小值;如果不存在,请说明理由.
是否存在外接圆,如果存在,求出外接圆面积的最小值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列![]() 的公差
的公差![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() ,且
,且![]() ,
,![]() .若实数
.若实数![]() ,则称
,则称![]() 具有性质
具有性质![]() .
.
(1)请判断![]() 、
、![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(2)设![]() 为数列
为数列![]() 的前
的前![]() 项和,
项和,![]() ,且
,且![]()
![]() 恒成立.求证:对任意的
恒成立.求证:对任意的![]()
![]() ,实数
,实数![]() 都不具有性质
都不具有性质![]() ;
;
(3)设![]() 是数列
是数列![]() 的前
的前![]() 项和,若对任意的
项和,若对任意的![]() ,
,![]() 都具有性质
都具有性质![]() ,求所有满足条件的
,求所有满足条件的![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,过
,过![]() 的焦点且垂直于
的焦点且垂直于![]() 轴的直线被
轴的直线被![]() 截得的弦长为
截得的弦长为![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)经过右焦点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,线段
两点,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴相交于点
轴相交于点![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项的和为
项的和为![]() ,记
,记![]() .
.
(1)若![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,其中
的等差数列,其中![]() ,
,![]() 均为正数.
均为正数.
①当![]() ,
,![]() ,
,![]() 成等差数列时,求
成等差数列时,求![]() 的值;
的值;
②求证:存在唯一的正整数![]() ,使得
,使得![]() .
.
(2)设数列![]() 是公比为
是公比为![]() 的等比数列,若存在
的等比数列,若存在![]() ,
,![]() (
(![]() ,
,![]() ,
,![]() )使得
)使得![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
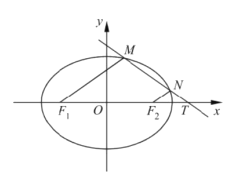
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() (a>b>0)的左、右焦点分别为
(a>b>0)的左、右焦点分别为![]() ,
,![]() . 已知
. 已知![]() 和
和![]() 都在椭圆上,其中
都在椭圆上,其中![]() 为椭圆的离心率.
为椭圆的离心率.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过![]() 作斜率为
作斜率为![]()
![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点(
两点(![]() 点在
点在![]() 点的左侧),且
点的左侧),且![]() . 若
. 若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com