
分析 (1)求出M的轨迹方程,利用点Q满足$\overrightarrow{QM}=\overrightarrow{MF}$,求动点Q的轨迹C的方程;
(2)确定0<y0<1,|x1-x2|≥4$\sqrt{2}$,即可求平面图形OAFB面积的最小值.
解答 解:(1)设M(a,b),则|b|=$\sqrt{{a}^{2}+(b-2)^{2}}$,
∴a2=4b-4,
设Q(x,y),则
∵点Q满足$\overrightarrow{QM}=\overrightarrow{MF}$,
∴a=$\frac{1}{2}$x,b=$\frac{1}{2}$(y+2),
∴$\frac{1}{4}$x2=2y,
∴x2=8y….(2分)
(2)联立直线l与抛物线方程可得y0x2+8x0x-8=0,
由题意可得-$\frac{8}{{y}_{0}}$<0,故0<y0<1,…..(8分)
设点A(x1,y1),B(x2,y2).
则x1+x2=-$\frac{8{x}_{0}}{{y}_{0}}$,x1x2=-$\frac{8}{{y}_{0}}$,且x02+y02=1,…(10分)
∴|x1-x2|2=$\frac{64{{x}_{0}}^{2}}{{{y}_{0}}^{2}}+\frac{32}{{y}_{0}}$=32[2$(\frac{1}{{y}_{0}}+\frac{1}{4})^{2}-\frac{17}{8}$]≥32,….(14分)
当且仅当y0=1时取“=”,
∴|x1-x2|≥4$\sqrt{2}$,
∴S=$\frac{1}{2}$|OF||x1-x2|≥4$\sqrt{2}$,…..(15分)
即平面图形OAFB面积的最小值为4$\sqrt{2}$…..(16分)
点评 本题考查抛物线方程,考查直线与抛物线的位置关系,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | -5 | C. | -4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
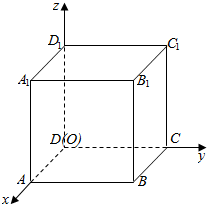 如图所示,以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图建立空间直角坐标系,则与$\overrightarrow{{A}_{1}C}$共线的向量的坐标可以是( )
如图所示,以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图建立空间直角坐标系,则与$\overrightarrow{{A}_{1}C}$共线的向量的坐标可以是( )| A. | (1,$\sqrt{2}$,$\sqrt{2}$) | B. | (1,1,$\sqrt{2}$) | C. | ($\sqrt{2}$,-$\sqrt{2}$,$\sqrt{2}$) | D. | ($\sqrt{2}$,$\sqrt{2}$,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com