
【题目】在△ABC中,角A、B、C的对边分别为a、b、c,且 ![]() ,B=C. (Ⅰ)求cosB的值;
,B=C. (Ⅰ)求cosB的值;
(Ⅱ)设函数f(x)=sin(2x+B),求 ![]() 的值.
的值.
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:高中数学 来源: 题型:
【题目】在公差大于0的等差数列{an}中,2a7﹣a13=1,且a1 , a3﹣1,a6+5成等比数列,则数列{(﹣1)n﹣1an}的前21项和为( )
A.21
B.﹣21
C.441
D.﹣441
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公比为正数的等比数列{an}(n∈N*),首项a1=3,前n项和为Sn , 且S3+a3、S5+a5、S4+a4成等差数列.
(1)求数列{an}的通项公式;
(2)设bn= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N.
,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N. 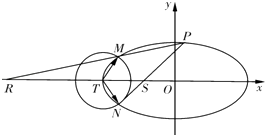
(1)求椭圆C的方程;
(2)求 ![]() 的最小值,并求此时圆T的方程;
的最小值,并求此时圆T的方程;
(3)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与x轴交于点R,S,O为坐标原点,求证:|OR||OS|为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在△ABC中,A,B的坐标分别为(-1,2),(4,3),AC的中点M在y轴上,BC的中点N在x轴上.
(1)求点C的坐标;
(2)求直线MN的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论:
①方程k= ![]() 与方程y-2=k(x+1)可表示同一直线;
与方程y-2=k(x+1)可表示同一直线;
②直线l过点P(x1 , y1),倾斜角为 ![]() ,则其方程为x=x1;
,则其方程为x=x1;
③直线l过点P(x1 , y1),斜率为0,则其方程为y=y1;
④所有直线都有点斜式和斜截式方程.
其中正确的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点M(2,2),N(5,-2),点P在x轴上,分别求满足下列条件的点P的坐标.
(1)∠MOP=∠OPN(O是坐标原点).
(2)∠MPN是直角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com