
【题目】已知函数![]() 且在
且在![]() 上的最大值为
上的最大值为![]() ,
,
(1)求函数f(x)的解析式;
(2)判断函数f(x)在(0,π)内的零点个数,并加以证明
【答案】(1)![]() (2)2个零点.
(2)2个零点.
【解析】
(1)由题意,可借助导数研究函数![]() 上的单调性,确定出最值,令最值等于
上的单调性,确定出最值,令最值等于![]() ,即可得到关于a的方程,由于a的符号对函数的最值有影响,故可以对a的取值范围进行讨论,分类求解;(2)借助导数研究函数f(x)在(0,π)内单调性,由零点判定定理即可得出零点的个数.
,即可得到关于a的方程,由于a的符号对函数的最值有影响,故可以对a的取值范围进行讨论,分类求解;(2)借助导数研究函数f(x)在(0,π)内单调性,由零点判定定理即可得出零点的个数.
(1)由已知得f′(x)=a(sinx+xcosx),对于任意的x∈(0, ![]() ),
),
有sinx+xcosx>0,当a=0时,f(x)= ![]() ,不合题意;
,不合题意;
当a<0时,x∈(0,![]() ),f′(x)<0,从而f(x)在(0,
),f′(x)<0,从而f(x)在(0, ![]() )单调递减,
)单调递减,
又函数f(x)=axsinx![]() (a∈R)在[0,
(a∈R)在[0, ![]() ]上图象是连续不断的,
]上图象是连续不断的,
故函数在[0, ![]() ]上的最大值为f(0),不合题意;
]上的最大值为f(0),不合题意;
当a>0时,x∈(0, ![]() ),f′(x)>0,从而f(x)在(0,
),f′(x)>0,从而f(x)在(0, ![]() )单调递增,
)单调递增,
又函数f(x)=axsinx ![]() (a∈R)在[0,
(a∈R)在[0, ![]() ]上图象是连续不断的,
]上图象是连续不断的,
故函数在[0, ![]() ]上上的最大值为f(
]上上的最大值为f(![]() )=
)=![]() a
a![]() =
=![]() ,解得a=1,
,解得a=1,
综上所述,得![]() ;
;
(2)函数f(x)在(0,π)内有且仅有两个零点。证明如下:
由(I)知,f(x)=xsinx![]() ,从而有f(0)=
,从而有f(0)= ![]() <0,f(
<0,f(![]() )=π32>0,
)=π32>0,
又函数在[0, ![]() ]上图象是连续不断的,所以函数f(x)在(0,
]上图象是连续不断的,所以函数f(x)在(0, ![]() )内至少存在一个零点,
)内至少存在一个零点,
又由(I)知f(x)在(0, ![]() )单调递增,故函数f(x)在(0,
)单调递增,故函数f(x)在(0, ![]() )内仅有一个零点。
)内仅有一个零点。
当x∈[![]() ,π]时,令g(x)=f′(x)=sinx+xcosx,
,π]时,令g(x)=f′(x)=sinx+xcosx,
由g(![]() )=1>0,g(π)=π<0,且g(x)在[
)=1>0,g(π)=π<0,且g(x)在[![]() ,π]上的图象是连续不断的,
,π]上的图象是连续不断的,
故存在m∈![]() ,π),使得g(m)=0.
,π),使得g(m)=0.
由g′(x)=2cosxxsinx,知x∈(![]() ,π)时,有g′(x)<0,
,π)时,有g′(x)<0,
从而g(x)在[![]() ,π]上单调递减。
,π]上单调递减。
当x∈![]() ,m),g(x)>g(m)=0,即f′(x)>0,
,m),g(x)>g(m)=0,即f′(x)>0,
从而f(x)在(![]() ,m)内单调递增
,m)内单调递增
故当x∈(![]() ,m)时,f(x)>f(π2)=π32>0,
,m)时,f(x)>f(π2)=π32>0,
从而(x)在(![]() ,m)内无零点;
,m)内无零点;
当x∈(m,π)时,有g(x)<g(m)=0,即f′(x)<0,
从而f(x)在(![]() ,m)内单调递减。
,m)内单调递减。
又f(m)>0,f(π)<0且f(x)在[m,π]上的图象是连续不断的,
从而f(x)在[m,π]内有且仅有一个零点。
综上所述,函数f(x)在(0,π)内有且仅有两个零点。


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,a=2![]() ,_______,求△ABC的周长l的范围.
,_______,求△ABC的周长l的范围.
在①![]() (﹣cos
(﹣cos![]() ,sin
,sin![]() ),
),![]() (cos
(cos![]() ,sin
,sin![]() ),且
),且![]()
![]() ,②cosA(2b﹣c)=acosC,③f(x)=cosxcos(x
,②cosA(2b﹣c)=acosC,③f(x)=cosxcos(x![]() )
)![]() ,f(A)
,f(A)![]()
注:这三个条件中任选一个,补充在上面问题中并对其进行求解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将含有甲、乙、丙的6名医护人员平均分成两组到A、B两家医院参加“防疫救护”工作,则甲、乙至少有一人在A医院且甲、丙不在同一家医院参加“防疫救护”工作的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种电子产品,每件产品合格的概率均为![]() ,现工厂为提高产品声誉,要求在交付用户前每件产品都通过合格检验,已知该工厂的检验仪器一次最多可检验
,现工厂为提高产品声誉,要求在交付用户前每件产品都通过合格检验,已知该工厂的检验仪器一次最多可检验![]() 件该产品,且每件产品检验合格与否相互独立.若每件产品均检验一次,所需检验费用较多,该工厂提出以下检验方案:将产品每
件该产品,且每件产品检验合格与否相互独立.若每件产品均检验一次,所需检验费用较多,该工厂提出以下检验方案:将产品每![]() 个(
个(![]() )一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验一次或
)一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验一次或![]() 次.设该工厂生产
次.设该工厂生产![]() 件该产品,记每件产品的平均检验次数为
件该产品,记每件产品的平均检验次数为![]() .
.
(1)![]() 的分布列及其期望;
的分布列及其期望;
(2)(i)试说明,当![]() 越大时,该方案越合理,即所需平均检验次数越少;
越大时,该方案越合理,即所需平均检验次数越少;
(ii)当![]() 时,求使该方案最合理时
时,求使该方案最合理时![]() 的值及
的值及![]() 件该产品的平均检验次数.
件该产品的平均检验次数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一位发烧病人的体温记录折线图,下列说法不正确的是( )
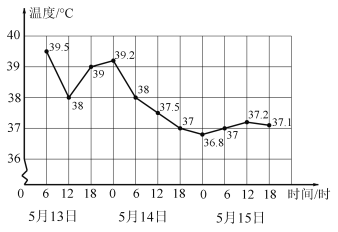
A.病人在5月13日12时的体温是![]()
![]()
B.病人体温在5月14日0时到6时下降最快
C.从体温上看,这个病人的病情在逐渐好转
D.病人体温在5月15日18时开始逐渐稳定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() 有下述四个结论:
有下述四个结论:
①函数![]() 的图象把圆
的图象把圆![]() 的面积两等分
的面积两等分
②![]() 是周期为
是周期为![]() 的函数
的函数
③函数![]() 在区间
在区间![]() 上有3个零点
上有3个零点
④函数![]() 在区间
在区间![]() 上单调递减
上单调递减
其中所有正确结论的编号是( )
A.①③④B.②④C.①④D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】厂家在产品出厂前,需对产品做检验,厂家将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收这批产品.
(1)若厂家库房中(视为数量足够多)的每件产品合格的概率为 ![]() 从中任意取出 3件进行检验,求至少有
从中任意取出 3件进行检验,求至少有![]() 件是合格品的概率;
件是合格品的概率;
(2)若厂家发给商家![]() 件产品,其中有
件产品,其中有![]() 不合格,按合同规定 商家从这
不合格,按合同规定 商家从这![]() 件产品中任取
件产品中任取![]() 件,都进行检验,只有
件,都进行检验,只有![]() 件都合格时才接收这批产品,否则拒收.求该商家可能检验出的不合格产品的件数ξ的分布列,并求该商家拒收这批产品的概率.
件都合格时才接收这批产品,否则拒收.求该商家可能检验出的不合格产品的件数ξ的分布列,并求该商家拒收这批产品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别是
的左、右焦点分别是![]() 、
、![]() ,离心率
,离心率![]() ,过点
,过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 、
、![]() 两点,
两点, ![]() 的周长为16.
的周长为16.
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 为原点,圆
为原点,圆![]() :
: ![]() (
(![]() )与椭圆
)与椭圆![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 为椭圆
为椭圆![]() 上一动点,若直线
上一动点,若直线![]() 、
、![]() 与
与![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,求证:
两点,求证: ![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com