科目：高中数学 来源： 题型：填空题
在等比数列{an}中，若a10＝0，则有等式
a1＋a2＋…＋an＝a1＋a2＋…＋a19－n(n<19，n∈N*)成立．类比上述性质，相应地，在等比数列{bn}中，若b9＝1，则等式______________成立 
查看答案和解析>>
科目：高中数学 来源： 题型：填空题
下列表述：①综合法是执因导果法；②综合法是顺推法；③分析法是执果索因法；④分析法是间接证法；⑤反证法是逆推法。正确的语句有是______(填序号)。
查看答案和解析>>
科目：高中数学 来源： 题型：填空题
观察下列等式：
12=1，
12—22=—3，
12—22+32=6，
12—22+32—42=-10，
…………………
由以上等式推测到一个一般的结论：对于
，12—22+32—42+…+（—1）n+1n2=
查看答案和解析>>
科目：高中数学 来源： 题型：填空题
边长为
的等边三角形内任一点到三边距离之和为定值，则这个定值为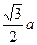
；
推
广到空间，棱长为的正四面体内任一点到各面距离之和为___________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
”时，从“
”变到 “
”时，左边应增乘的因式
是________________
_____ ；
中，两直角边分别为
、
，设
为斜边上的高，则
，由此类比：三棱锥
中的三条侧棱
、
、
两两垂直，且长度分别为
，设棱锥底面
上的高为
是等比数列，
是互不相等的正整数，则有正确的结论：
．类比上述性质，相应地，若
是等差数列，