
| A. | $f(x)=\sqrt{x^2}$,g(x)=x | B. | $f(x)=\sqrt{{x^2}-4},g(x)=\sqrt{x+2}\sqrt{x-2}$ | ||
| C. | $f(x)=x,g(x)=\frac{x^2}{x}$ | D. | f(x)=|x+1|,g(x)=$\left\{\begin{array}{l}{x+1,x≥-1}\\{-x-1,x-1}\end{array}\right.$ |
分析 根据两个函数的定义域相同,对应关系也相同,判断它们是同一函数.
解答 解:对于A,f(x)=$\sqrt{{x}^{2}}$=|x|,与g(x)=x的对应关系不同,∴不是同一函数;
对于B,f(x)=$\sqrt{{x}^{2}-4}$(x≥2或x≤-2),与g(x)=$\sqrt{x+2}$$\sqrt{x-2}$=$\sqrt{{x}^{2}-4}$(x≥2)的定义域不同,
∴不是同一函数;
对于C,f(x)=x(x∈R),与g(x)=$\frac{{x}^{2}}{x}$=x(x≠0)的定义域不同,∴不是同一函数;
对于D,f(x)=|x+1|=$\left\{\begin{array}{l}{x+1,x≥-1}\\{-x-1,x<-1}\end{array}\right.$,与g(x)=$\left\{\begin{array}{l}{x+1,x≥-1}\\{-x-1,x<-1}\end{array}\right.$的定义域相同,
对应关系也相同,是同一函数.
故选:D.
点评 本题考查了判断两个函数是否为同一函数的应用问题,是基础题目.


科目:高中数学 来源: 题型:选择题
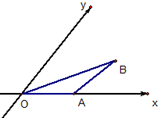
| A. | 等边三角形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,m∥n,则n∥α | B. | 若m⊥α,n⊥β,则m⊥n | C. | 若m⊥α,m∥β,则α⊥β | D. | 若α⊥β,n?α,则n⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4018 | B. | 4019 | C. | 4020 | D. | 4021 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com