【题目】甲乙两地的高速公路全长166千米，汽车从甲地进入该高速公路后匀速行驶到乙地，车速
（千米/时）.已知汽车每小时的运输成本（以元为单位）由可变部分和固定部分组成：可变部分为
，固定部分为220元.
(1)把全程运输成本
（元）表示为速度
（千米/时）的函数，并指出这个函数的定义域；
(2)汽车应以多大速度行驶才能使全程运输成本最小？最小运输成本为多少元？（结果保留整数）
【答案】(1)
；(2)当
时，最小运输成本为696元.
【解析】
(1)由题意可知，汽车的行驶时间为
（小时），汽车每小时的运输成本为
，从而确定全程运输成本
（元）表示为速度
（千米/时）的函数关系，即可.
(2)由(1)可知，
，根据对号函数，求解即可.
(1)因为汽车从甲地进入该高速公路后匀速行驶到乙地，车速
（千米/时）.
所以汽车的行驶时间为（小时）
又汽车每小时的运输成本（以元为单位）由可变部分和固定部分组成：可变部分为
，固定部分为220元
所以汽车每小时的运输成本为
（元）
则全程运输成本
(2) 由(1)可知，
当
时，函数
单调递减
当
时，函数单调递增
所以，当
时，全程运输成本取得最小值
即最小运输成本为
元.
轻松夺冠全能掌控卷系列答案科目：高中数学 来源： 题型：
【题目】已知椭圆C：
过点A
，两个焦点为（-1，0），（1，0）。
（Ⅰ）求椭圆C的方程；
（Ⅱ）E,F是椭圆C上的两个动点，如果直线AE的斜率与AF的斜率互为相反数，证明直线EF的斜率为定值，并求出这个定值。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示是一个几何体的直观图、正视图、俯视图、侧视图(其中正视图为直角梯形，俯视图为正方形，侧视图为直角三角形，尺寸如图所示)．
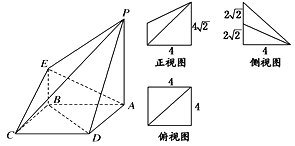
(1)求四棱锥P-ABCD的体积；
(2)证明：BD∥平面PEC；
(3)线段BC上是否存在点M，使得AE⊥PM？若存在，请说明其位置，并加以证明；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，
为函数
的导函数．
(1)若
，函数
在
处的切线方程为
，求a、
的值；
(2)若曲线
上存在两条互相平行的切线，其倾斜角为锐角，求实数
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】人的正常体温在
至
之间，下图是一位病人在治疗期间的体温变化图.
现有下述四个结论：
①此病人已明显好转；
②治疗期间的体温极差小于
；
③从每8小时的变化来看，25日0时~8时体温最稳定；
④从3月22日8时开始，每8小时量一次体温，若体温不低于
就服用退烧药，根据图中信息可知该病人服用了3次退烧药.
其中所有正确结论的编号是（ ）
A.③④B.②③C.①②④D.①②③
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列
的前
项和为
，且满足
；数列
的前项和为
，且满足
，
，
．
（1）求数列的通项公式；
（2）求数列的通项公式；
（3）是否存在正整数，使得
恰为数列中的一项？若存在，求满足要求的那几项；若不存在，说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
