
分析 由题意可得 x=$\frac{2\sqrt{5}}{5}$,y=$-\frac{\sqrt{5}}{5}$,r=$\sqrt{{x}^{2}+{y}^{2}}$=1,由此求得cosα=$\frac{x}{r}$ 的值.
解答 解:∵角α的终边经过点($\frac{2\sqrt{5}}{5},-\frac{\sqrt{5}}{5}$),
∴x=$\frac{2\sqrt{5}}{5}$,y=$-\frac{\sqrt{5}}{5}$,
∴r=$\sqrt{{x}^{2}+{y}^{2}}$=1,
∴cosα=$\frac{x}{r}$=x=$\frac{2\sqrt{5}}{5}$,
故答案为:$\frac{2\sqrt{5}}{5}$
点评 本题主要考查任意角的三角函数的定义,属于基础题.


科目:高中数学 来源: 题型:解答题
 如图,直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,∠ACB=90°,且AC=AA1.
如图,直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,∠ACB=90°,且AC=AA1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
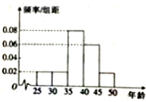 2015年某企业员工有500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.现在要从年龄较小的第1,3,4组中用分层抽样的方法抽取16人,则在第4组抽取的人数为( )
2015年某企业员工有500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.现在要从年龄较小的第1,3,4组中用分层抽样的方法抽取16人,则在第4组抽取的人数为( )| A. | 3 | B. | 6 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知函数f(x)=$\sqrt{3}$sin(ωx+φ)(ω>0,-π<φ<π)的部分图象如图所示,为了得到g(x)=$\sqrt{3}$cos(ωx+$\frac{φ}{2}$)的图象,只需将f(x)的图象( )
已知函数f(x)=$\sqrt{3}$sin(ωx+φ)(ω>0,-π<φ<π)的部分图象如图所示,为了得到g(x)=$\sqrt{3}$cos(ωx+$\frac{φ}{2}$)的图象,只需将f(x)的图象( )| A. | 向左平移$\frac{5π}{12}$个单位长度 | B. | 向左平移$\frac{5π}{6}$个单位长度 | ||
| C. | 向右平移$\frac{5π}{12}$个单位长度 | D. | 向右平移$\frac{5π}{6}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0 | 0.5 | 0.53125 | 0.5625 | 0.625 | 0.75 | 1 |
| f(x) | -1.307 | -0.084 | -0.009 | 0.066 | 0.215 | 0.512 | 1.099 |
| A. | 0.625 | B. | -0.009 | C. | 0.5625 | D. | 0.066 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com