一个盒子中装有4张卡片.每张卡片上写有1个数字.数字分别是1.2.3.4.现从盒子中随机抽取卡片．(I)若一次抽取3张卡片.求3张卡片上数字之和大于7的概率,(II)若第一次抽1张卡片.放回后再抽取1张卡片.求两次抽取中至少一次抽到数字3的概率．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

（10分）一个盒子中装有4张卡片，每张卡片上写有1个数字，数字分别是1、2、3、4。现从盒子中随机抽取卡片．
(I)若一次抽取3张卡片，求3张卡片上数字之和大于7的概率；
(II)若第一次抽1张卡片，放回后再抽取1张卡片，求两次抽取中至少一次抽到数字3的概率．

（Ⅰ）P(A)=0.5；（Ⅱ）P(B)= 。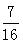

解析试题分析：（Ⅰ）由题意知本题是一个古典概型，
设A表示事件“抽取3张卡片上的数字之和大于7”，  ……1分
∵任取三张卡片，三张卡片上的数字全部可能的结果是{（1、2、3），（1、2、4），（1、3、4），（2、3、4）}共4个，        ……3分
其中数字之和大于7的是（1、3、4），（2、3、4），∴P(A)=0.5    ……5分
（Ⅱ）设B表示事件“至少一次抽到3”，  ……6分
∵每次抽1张，连续抽取两张全部可能的基本结果有：
（1、1）（1、2）（1、3）（1、4）（2、1）（2、2）（2、3）（2、4）（3、1）（3、2）（3、3）（3、4）（4、1）（4、2）（4、3）（4、4），共16个．    ……8分
事件B包含的基本结果有（1、3）（2、3）（3、1）（3、2）（3、3）（3、4）（4、3），共7个基本结果．∴所求事件的概率为P(B)= 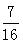      ……10分
考点：本题主要考查古典概型的概率计算。
点评：中档题，古典概型概率的计算，关键是明确基本事件总数及导致事件发生的基本事件数，此类问题，可借助于“树图法”不重不漏地写出各个基本事件。

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

一袋中有6个黑球，4个白球．
(1)依次取出3个球，不放回，已知第一次取出的是白球，求第三次取到黑球的概率；
(2)有放回地依次取出3球，已知第一次取的是白球，求第三次取到黑球的概率；
(3)有放回地依次取出3球，求取到白球个数X的分布列、期望和方差．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

（本题满分12分）因金融危机，某公司的出口额下降，为此有关专家提出两种促进出口的方案，每种方案都需要分两年实施．若实施方案一，预计第一年可以使出口额恢复到危机前的1．0倍、0．9倍、0．8倍的概率分别为0．3、0．3、0．4；第二年可以使出口额为第一年的1．25倍、1．0倍的概率分别是0．5、0．5．若实施方案二，预计第一年可以使出口额恢复到危机前的1．2倍、l．0倍、0．8倍的概率分别为0．2、0．3、0．5；第二年可以使出口额为第一年的1．2倍、1．0倍的概率分别是0．4、0．6．实施每种方案第一年与第二年相互独立．令ζ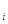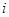（=1，2）表示方案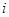实施两年后出口额达到危机前的倍数。
（Ⅰ）写出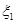、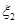的分布列；
（Ⅱ）实施哪种方案，两年后出口额超过危机前出口额的概率更大?
（Ⅲ）不管哪种方案，如果实施两年后出口额达不到、恰好达到、超过危机前出口额，预计利润分别为10万元、15万元、20万元，问实施哪种方案的平均利润更大。

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

（本小题满分13分）
设a、b、c分别是先后掷一枚质地均匀的正方体骰子三次得到的点数.
（1）求使函数在R上不存在极值点的概率；
（2）设随机变量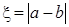，求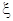的分布列和数学期望.

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

二十世纪50年代，日本熊本县水俣市的许多居民都患了运动失调、四肢麻木等症状，人们把它称为水俣病．经调查发现一家工厂排出的废水中含有甲基汞，使鱼类受到污染．人们长期食用含高浓度甲基汞的鱼类引起汞中毒．引起世人对食品安全的关注．《中华人民共和国环境保护法》规定食品的汞含量不得超过1.00ppm．
罗非鱼是体型较大，生命周期长的食肉鱼，其体内汞含量比其他鱼偏高．现从一批罗非鱼中随机地抽出15条作样本，经检测得各条鱼的汞含量的茎叶图（以小数点前一位数字为茎，小数点后一位数字为叶）如下：

（Ⅰ）若某检查人员从这15条鱼中，随机地抽出3条，求恰有1条鱼汞含量超标的概率；
（Ⅱ）以此15条鱼的样本数据来估计这批鱼的总体数据．若从这批数量很大的鱼中任选3条鱼，记ξ表示抽到的鱼汞含量超标的条数，求ξ的分布列及Eξ

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

一个盒子中有5只同型号的灯泡，其中有3只合格品，2只不合格品。现在从中依次取出2只，设每只灯泡被取到的可能性都相同，请用“列举法”解答下列问题：
（1）求第一次取到不合格品，且第二次取到的是合格品的概率；
（2）求至少有一次取到不合格品的概率。

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

盒中有6只灯泡,其中有2只是次品,4只是正品.从中任取2只,试求下列事件的概率．
(Ⅰ)取到的2只都是次品；
(Ⅱ)取到的2只中恰有一只次品.

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

甲、乙、丙三人独立地对某一技术难题进行攻关。甲能攻克的概率为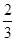，乙能攻克的概率为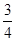，丙能攻克的概率为.
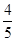（1）求这一技术难题被攻克的概率；
（2）若该技术难题末被攻克，上级不做任何奖励；若该技术难题被攻克，上级会奖励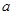万元。奖励规则如下：若只有1人攻克，则此人获得全部奖金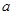万元；若只有2人攻克，则奖金奖给此二人，每人各得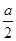万元；若三人均攻克，则奖金奖给此三人，每人各得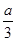万元。设甲得到的奖金数为X，求X的分布列和数学期望。（本题满分12分）