
【题目】如图,为方便金湖县人民游览三河风景区附近的“网红桥”,现准备在河岸一侧建造一个观景台A,已知射线PM, PN为两边夹角为120°的公路(长度均超过5千米),在两条公路PM,PN上分别设立游客上下点B、C,在观景台A和游客上下点B、C之间和游客上下点B、C之间分别建造三条观光线路AB,AC,BC,测得PB=3干米,PC=5千米.

(1)求线段BC的长度;
(2)若∠BAC= 60°,因政府要计算修建三条观光线路所需费用,所以要计算AB,AC,BC三条线路的总长度的取值范围,请你建立合适的数学模型,帮助政府解决这个问题.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,离心率
,离心率![]() .
.
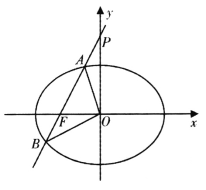
(I)求椭圆C的标准方程;
(II)已知直线![]() 交椭圆C于A,B两点.
交椭圆C于A,B两点.
①若直线![]() 经过椭圆C的左焦点F,交y轴于点P,且满足
经过椭圆C的左焦点F,交y轴于点P,且满足![]() .求证:
.求证:![]() 为定值;
为定值;
②若![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知(b-c)2=a2-![]() bc.
bc.
(1)求sinA;
(2)若a=2,且sinB,sinA,sinC成等差数列,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点重合,且过点
的焦点重合,且过点![]() .过点
.过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,
两点, ![]() 为椭圆的左顶点.
为椭圆的左顶点.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)求![]() 面积的最大值,并求此时直线
面积的最大值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举行运动会,其中三级跳远的成绩在8.0米(四舍五入,精确到0.1米)以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.

(1)求进入决赛的人数;
(2)经过多次测试后发现,甲成绩均匀分布在8~10米之间,乙成绩均匀分布在8.5~10.5米之间,现甲,乙各跳一次,求甲比乙远的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() x3﹣
x3﹣![]() x2+x,a∈R.
x2+x,a∈R.
(Ⅰ)当a=1时,求f(x)在[﹣1,1]上的最大值和最小值;
(Ⅱ)若f(x)在区间[![]() ,2]上单调递增,求a的取值范围;
,2]上单调递增,求a的取值范围;
(Ⅲ)当m<0时,试判断函数g(x)=![]() -
-![]() 其中f′(x)是f(x)的导函数)是否存在零点,并说明理由.
其中f′(x)是f(x)的导函数)是否存在零点,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,
,![]() 在椭圆上.
在椭圆上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知动直线![]() (斜率存在)与椭圆相交于点
(斜率存在)与椭圆相交于点![]() 两点,且
两点,且![]() 的面积
的面积![]() ,若
,若![]() 为线段
为线段![]() 的中点.
的中点.![]() 点在
点在![]() 轴上投影为
轴上投影为![]() ,问:在
,问:在![]() 轴上是否存在两个定点
轴上是否存在两个定点![]() ,使得
,使得![]() 为定值,若存在求出
为定值,若存在求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com