
【题目】如图是一个表面被涂上红色的棱长是4cm的立方体,将其适当分割成棱长为1cm的小立方体.

(1)共得到多少个棱长是1cm的小立方体?
(2)三面是红色的小立方体有多少个?它们的表面积之和是多少?
(3)两面是红色的小立方体有多少个?它们的表面积之和是多少?
(4)一面是红色的小立方体有多少个?它们的表面积之和是多少?
(5)六个面均没有颜色的小立方体有多少个?它们的表面积之和是多少?它们占有多少立方厘米的空间?
【答案】(1)64个;
(2)8个, 48![]() ;
;
(3)24个, 144![]() ;
;
(4)24个, 144![]() ;
;
(5)8个, 48![]() , 8
, 8![]()
【解析】
(1)棱长是4![]() 的立方体体积64
的立方体体积64![]() ,棱长为1
,棱长为1![]() 的小正方体体积为1
的小正方体体积为1![]() ,由此能求出共得到多少个棱长为1
,由此能求出共得到多少个棱长为1![]() 的小正方体;
的小正方体;
(2)三面涂色的小正方体是位于棱长是4![]() 的立方体的顶点处的小正方体,由此能求出三面涂色的小正方体有多少个,表面积之和为多少;
的立方体的顶点处的小正方体,由此能求出三面涂色的小正方体有多少个,表面积之和为多少;
(3)二面涂色的小正方体是位于棱长是4![]() 的立方体的各边上的正方体,由此能求出二面涂色的小正方体有多少个,表面积之和为多少;
的立方体的各边上的正方体,由此能求出二面涂色的小正方体有多少个,表面积之和为多少;
(5)六个面均没涂色的小正方体为棱长是4![]() 的立方体中心的正方体,由此能求出六个面均没有涂色的小正方体有多少个,表面积之和为多少,它们占有多少立方厘米.
的立方体中心的正方体,由此能求出六个面均没有涂色的小正方体有多少个,表面积之和为多少,它们占有多少立方厘米.
解:(1)棱长是4![]() 的立方体体积为:4×4×4=64(
的立方体体积为:4×4×4=64(![]() ),
),
棱长为1![]() 的小正方体体积为1
的小正方体体积为1![]() ,
,
∴共得到![]() 个小正方体;
个小正方体;
(2)三面涂色的小正方体是位于棱长是4![]() 的立方体的顶点处的小正方体,
的立方体的顶点处的小正方体,
∵立方体共有8个顶点,
∴三面涂色的小正方体有8个,
每个小正方体的表面积为6![]() ,
,
则表面积之和为8×6=48(![]() );
);
(3)二面涂色的小正方体是位于棱长是4![]() 的立方体的各边上的正方体,
的立方体的各边上的正方体,
∵立方体共有12条边,每边有2个正方体,
∴二面涂色的小正方体有24个,
每个小正方体的表面积为6![]() ,
,
则表面积之和为24×6=144(![]() );
);
(4)一面涂色的小正方体在棱长是4![]() 的立方体的表面上既不是顶点又不是各边上的正方体,
的立方体的表面上既不是顶点又不是各边上的正方体,
∵立方体共有6个面,每个面有4个正方体,
∴一面涂色的小正方体有24个,
每个小正方体的表面积为6![]() ,
,
则表面积之和为24×6=144(![]() );
);
(5)六个面均没涂色的小正方体为棱长是4![]() 的立方体中心的正方体,
的立方体中心的正方体,
共有6482424=8个,
每个小正方体的表面积为6![]() ,
,
则表面积之和为8×6=48(![]() ),
),
它们占8×1=8(![]() )的空间.
)的空间.


科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合P={x|x(x-2)≥0},M={x|a<x<a+3}.
(1)求集合UP;
(2)若a=1,求集合P∩M;
(3)若UPM,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1:y=cos x,C2:y=sin (2x+![]() ),则下面结论正确的是( )
),则下面结论正确的是( )
A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() ,(
,(![]() 为参数),以原点为极点,
为参数),以原点为极点,![]() 轴的正半轴为极轴建立极坐标轴,曲线
轴的正半轴为极轴建立极坐标轴,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解学生考试时的紧张程度,现对100名同学进行评估,打分区间为![]() ,得到频率分布直方图如下,其中
,得到频率分布直方图如下,其中![]() 成等差数列,且
成等差数列,且![]() .
.

(1)求![]() 的值;
的值;
(2)现采用分层抽样的方式从紧张度值在![]() ,
,![]() 中共抽取5名同学,再从这5名同学中随机抽取2人,求至少有一名同学是紧张度值在
中共抽取5名同学,再从这5名同学中随机抽取2人,求至少有一名同学是紧张度值在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《最强大脑》是江苏卫视引进德国节目《SuperBrain》而推出的大型科学竞技真人秀节目.节目筹备组透露挑选选手的方式:不但要对空间感知、照相式记忆进行考核,而且要让选手经过名校最权威的脑力测试,120分以上才有机会入围.某重点高校准备调查脑力测试成绩是否与性别有关,在该高校随机抽取男、女学生各100名,然后对这200名学生进行脑力测试.规定:分数不小于120分为“入围学生”,分数小于120分为“未入围学生”.已知男生入围24人,女生未入围80人.
(1)根据题意,填写下面的![]() 列联表,并根据列联表判断是否有
列联表,并根据列联表判断是否有![]() 以上的把握认为脑力测试后是否为“入围学生”与性别有关;
以上的把握认为脑力测试后是否为“入围学生”与性别有关;
性别 | 入围人数 | 未入围人数 | 总计 |
男生 | 24 | ||
女生 | 80 | ||
总计 |
(2)用分层抽样的方法从“入围学生”中随机抽取11名学生,然后再从这11名学生中抽取3名参加某期《最强大脑》,设抽到的3名学生中女生的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附: ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
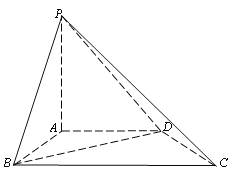
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥AD,AD∥BC,AP=AB=AD=1.
(Ⅰ)若直线PB与CD所成角的大小为![]() ,求BC的长;
,求BC的长;
(Ⅱ)求二面角B-PD-A的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com