
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)当![]() 时,
时,![]() 在
在![]() 处取得极值,求函数
处取得极值,求函数![]() 的单调区间;
的单调区间;
(2)若![]() 时,函数
时,函数![]() 有两个不同的零点
有两个不同的零点![]() ,
,
①求![]() 的取值范围;
的取值范围;
②求证:![]() .
.
【答案】(Ⅰ)减区间为![]() ,增区间为
,增区间为![]() .(Ⅱ)①
.(Ⅱ)①![]() ②详见解析
②详见解析
【解析】试题分析:(Ⅰ)由极值定义可得![]() ,从而可解得
,从而可解得![]() .再根据导函数零点讨论导函数符号,结合导函数符号可得函数单调区间,(Ⅱ)①先利用导数分析函数单调性,即函数为非单调函数,导函数必有零点,再根据函数单调变化规律得函数最大值必大于零,又端点函数值趋于负无穷,根据零点存在定理可得函数必有两个零点,最后解最大值大于零时
.再根据导函数零点讨论导函数符号,结合导函数符号可得函数单调区间,(Ⅱ)①先利用导数分析函数单调性,即函数为非单调函数,导函数必有零点,再根据函数单调变化规律得函数最大值必大于零,又端点函数值趋于负无穷,根据零点存在定理可得函数必有两个零点,最后解最大值大于零时![]() 的取值范围,②
的取值范围,②![]() 等价于
等价于![]() ,由零点条件得
,由零点条件得![]() ,
,![]() ,两式相加与相减再相除消去
,两式相加与相减再相除消去![]() 得
得![]() ,因此转化为证明
,因此转化为证明![]() ,即需证明
,即需证明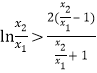 ,令
,令![]() ,构造函数
,构造函数![]() ,再利用导数研究函数单调性,得
,再利用导数研究函数单调性,得![]() ,即可得到结论.
,即可得到结论.
试题解析:(Ⅰ)解:由已知得![]() ,
,
所以![]() ,所以
,所以![]() .
.
所以![]() .
.
则![]() ,
,
由![]() 得
得![]() ,由
,由![]() 得
得![]() ./span>
./span>
所以![]() 的减区间为
的减区间为![]() ,增区间为
,增区间为![]() .
.
(Ⅱ)①解:由已知![]() .
.
所以![]() ,
,
当![]() 时,显然
时,显然![]() 恒成立,此时函数
恒成立,此时函数![]() 在定义域内递增,
在定义域内递增,![]() 至多有一个零点,不合题意.当
至多有一个零点,不合题意.当![]() 时,令
时,令![]() 得
得![]() ,
,
令![]() 得
得![]() ;
;
令![]() 得
得![]() .
.
所以![]() 极大值为
极大值为![]() ,解得
,解得![]() .
.
且![]() 时,
时,![]() ,
,![]() 时,
时,![]() .
.
所以当![]() 时,
时,![]() 有两个零点.
有两个零点.
②证明:![]() ,
,![]() 为函数
为函数![]() 的两个零点,不妨设
的两个零点,不妨设![]() .
.
所以![]() ,
,![]() ,
,
两式相减得![]() ,两式相加得
,两式相加得![]() .
.
要证![]() ,即证
,即证![]() ,
,
即证![]() ,即证
,即证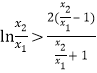 .
.
令![]() ,即证
,即证![]() .
.
令![]() ,则
,则![]() ,
,
所以![]() ,即
,即![]() ,
,
所以![]() ,所以
,所以![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】【2015高考四川,文21】已知函数f(x)=-2lnx+x2-2ax+a2,其中a>0.
(Ⅰ)设g(x)为f(x)的导函数,讨论g(x)的单调性;
(Ⅱ)证明:存在a∈(0,1),使得f(x)≥0恒成立,且f(x)=0在区间(1,+∞)内有唯一解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与圆C:
与圆C:![]() 相交于A,B两点,弦AB中点为M(0,1),
相交于A,B两点,弦AB中点为M(0,1),
(1)求实数![]() 的取值范围以及直线
的取值范围以及直线![]() 的方程;
的方程;
(2)若圆C上存在四个点到直线![]() 的距离为
的距离为![]() ,求实数a的取值范围;
,求实数a的取值范围;
(3)已知N(0,﹣3),若圆C上存在两个不同的点P,使![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年1月1日,作为贵阳市打造“千园之城”27个示范性公园之一的泉湖公园正式开园.元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放.现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:
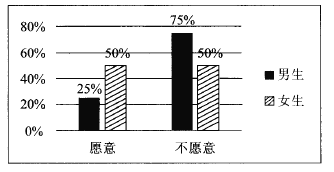
(1)根据条件完成下列![]()
列联表,并判断是否在犯错误的概率不超过1%的情况下愿意接受挑战与性别有关?
愿意 | 不愿意 | 总计 | |
男生 | |||
女生 | |||
总计 |
(2)水上挑战项目共有两关,主办方规定:挑战过程依次进行,每一关都有两次机会挑战,通过第一关后才有资格参与第二关的挑战,若甲参加每一关的每一次挑战通过的概率均为![]()
,记甲通过的关数为![]()
,求![]()
的分布列和数学期望.
参考公式与数据:
| 0.1 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |
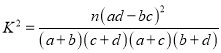
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列5个命题中正确命题的个数是( )
①对于命题p:x∈R,使得x2+x+1<0,则綈p:x∈R,均有x2+x+1>0;
②m=3是直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直的充要条件;
③已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则线性回归方程为![]() =1.23x+0.08;
=1.23x+0.08;
④若实数x,y∈[-1,1],则满足x2+y2≥1的概率为![]() ;
;
⑤曲线y=x2与y=x所围成图形的面积是S= (x-x2)dx.
A.2 B.3 C.4 D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一医用放射性物质原来质量为a,每年衰减的百分比相同,当衰减一半时,所用时间是10年,根据需要,放射性物质至少要保留原来的,否则需要更换.已知到今年为止,剩余的为原来的![]() ,
,
(1)求每年衰减的百分比;
(2)到今年为止,该放射性物质已衰减了多少年?
(3)今后至多还能用多少年?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com