
动圆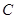 与定圆
与定圆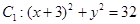 内切,与定圆
内切,与定圆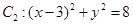 外切,A点坐标为
外切,A点坐标为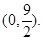 (1)求动圆
(1)求动圆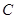 的圆心
的圆心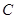 的轨迹方程和离心率;(2)若轨迹
的轨迹方程和离心率;(2)若轨迹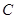 上的两点
上的两点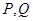 满足
满足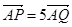 ,求
,求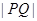 的值.
的值.
(1) ,离心率为
,离心率为 ;(2)
;(2) .
.
【解析】本试题主要是考查了运用定义法求解轨迹方程以及直线与圆锥曲线的位置关系的综合运用。
(1)利用圆与圆的位置关系,结合圆心距和半径的关系,得到动点的轨迹满足椭圆的定义,然后结合定义得到轨迹方程。
(2)设出直线方程与椭圆方程联立方程组,然后结合韦达定理和向量的关系式的,到坐标关系,进而化简得到点的坐标。
(1)如图,设动圆C的半径为R,

则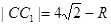 ,①
,①
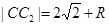 ,②
,②
①+②得,
由椭圆的定义知 点的轨迹是以
点的轨迹是以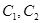 为焦点,长轴长为
为焦点,长轴长为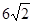 的椭圆,其轨迹方程为
的椭圆,其轨迹方程为 ,离心率为
,离心率为 ……………………………………………………………………6分
……………………………………………………………………6分
(2)设
由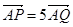 可得
可得
所以 ③…………………………………9分
③…………………………………9分
由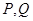 是椭圆
是椭圆 上的两点,得
上的两点,得
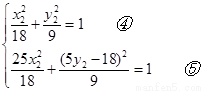 ,由④、⑤得
,由④、⑤得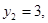
将 代入③,得
代入③,得 ,将
,将 代入④,得
代入④,得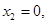 所以
所以 ,
,
所以 .…………………………………………13分
.…………………………………………13分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2012-2013学年天津市天津一中高二上学期期中考试理科数学试卷(带解析) 题型:解答题
动圆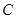 与定圆
与定圆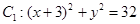 内切,与定圆
内切,与定圆 外切,A点坐标为
外切,A点坐标为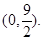 (1)求动圆
(1)求动圆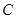 的圆心
的圆心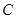 的轨迹方程和离心率;(2)若轨迹
的轨迹方程和离心率;(2)若轨迹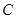 上的两点
上的两点 满足
满足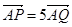 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2013届湖北省武汉市高二下期末文科数学试卷(解析版) 题型:解答题
(本小题满分14分)
动圆G与圆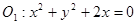 外切,同时与圆
外切,同时与圆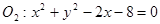 内切,设动圆圆心G的轨迹为
内切,设动圆圆心G的轨迹为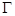 。
。
(1)求曲线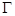 的方程;
的方程;
(2)直线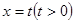 与曲线
与曲线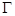 相交于不同的两点
相交于不同的两点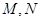 ,以
,以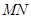 为直径作圆
为直径作圆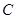 ,若圆C与
,若圆C与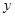 轴相交于两点
轴相交于两点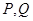 ,求
,求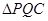 面积的最大值;
面积的最大值;
(3)设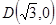 ,过
,过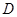 点的直线
点的直线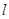 (不垂直
(不垂直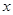 轴)与曲线
轴)与曲线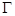 相交于
相交于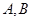 两点,与
两点,与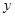 轴交于点
轴交于点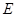 ,若
,若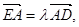
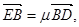 试探究
试探究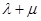 的值是否为定值,若是,求出该定值,若不是,请说明理由。
的值是否为定值,若是,求出该定值,若不是,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2013届江西省四校高二下学期第三次月考理科数学试卷(解析版) 题型:解答题
(本小题满分13分)
动圆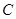 与定圆
与定圆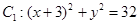 内切,与定圆
内切,与定圆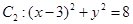 外切,A点坐标为
外切,A点坐标为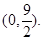
(1)求动圆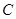 的圆心
的圆心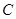 的轨迹方程和离心率;
的轨迹方程和离心率;
(2)若轨迹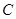 上的两点
上的两点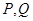 满足
满足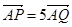 ,求
,求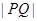 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com