
分析 通过换元转化为求二次函数的值域问题,先求出函数的对称轴,得到函数的单调区间,求出函数的最大值和最小值即可求出值域.
解答 解:由于函数f(x)=4x-2x+1=(2x)2-2x+1
令t=2x,由于x∈[-3,2],则t∈[$\frac{1}{8}$,4],
由f(t)=t2-t+1=(t-$\frac{1}{2}$)2+$\frac{3}{4}$
得:f(t)的对称轴是t=$\frac{1}{2}$,
∴函数在[$\frac{1}{8}$,$\frac{1}{2}$]递减,在[$\frac{1}{2}$,4]递增,
∴f(t)最小值=f($\frac{1}{2}$)=$\frac{3}{4}$,f(t)最大值=f(4)=13,
∴函数的值域是[$\frac{3}{4}$,13].
点评 本题考查了求函数的值域问题,考查二次函数的性质,是一道基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
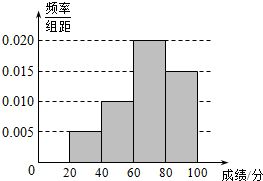 某班学生参加数学测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若低于60分的人数是18人,则该班的学生人数是( )
某班学生参加数学测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若低于60分的人数是18人,则该班的学生人数是( )| A. | 45 | B. | 50 | C. | 55 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=cos(x+$\frac{π}{2}$) | B. | y=1-2cos22x | C. | y=-x2 | D. | y=|sin(π-x)| |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
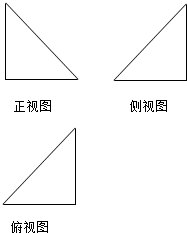 己知几何体的三视图如图所示,它们都是直角边长等于1的等腰直角三角形,则这个几何体的表面积等于( )
己知几何体的三视图如图所示,它们都是直角边长等于1的等腰直角三角形,则这个几何体的表面积等于( )| A. | 2 | B. | $\frac{{3+\sqrt{2}}}{2}$ | C. | 4 | D. | $\sqrt{2}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,0) | B. | (-$\frac{1}{2}$,0) | C. | (0,$\frac{1}{8}$) | D. | (0,-$\frac{1}{8}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$πR2 | B. | $\frac{9}{2}$πR2 | C. | $\frac{9}{4}$πR2 | D. | $\frac{9}{8}$πR2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com