
分析 (1)由椭圆离心率为$\frac{\sqrt{2}}{2}$,且一个焦点和短轴的两个端点构成面积为1的等腰直角三角形及b2=a2-c2即可得出椭圆的标准方程;
(2)由$\overrightarrow{OT}$=2$\overrightarrow{OM}$,可得M的坐标,从而可求线段MN的长;
(3)把直线l的方程与椭圆的方程联立,消去y得到关于x的一元二次方程,利用根与系数的关系及弦长公式即可得到|AB|,利用垂径定理及半径、弦长的一半、弦心距三者之间的关系得到|GH|,进而得出k.
解答 解:(1)∵椭圆离心率为$\frac{\sqrt{2}}{2}$,且一个焦点和短轴的两个端点构成面积为1的等腰直角三角形,
∴$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,$\frac{1}{2}$bc=1,b=c,
∴a=$\sqrt{2}$,b=c=1,
∴椭圆的标准方程为$\frac{{x}^{2}}{2}+{y}^{2}$=1;
(2)由题意可知xM=xF=c=1,
故将xM=1代入$\frac{{x}^{2}}{2}+{y}^{2}$=1,可得|yM|=$\frac{\sqrt{2}}{2}$,从而|MN|=$\sqrt{2}$.
(3)设A(x1,y1),B(x2,y2).
由直线l与椭圆C,消去y得到(1+2k2)x2-2=0,则x1+x2=0,x1x2=-$\frac{2}{1+2{k}^{2}}$.
∴|AB|=$\sqrt{\frac{8(1+{k}^{2})}{1+2{k}^{2}}}$.
点Q($\sqrt{2}$,0)到直线l的距离d=$\frac{|\sqrt{2}k|}{\sqrt{1+{k}^{2}}}$.
则|GH|=2$\sqrt{\frac{7}{3}-\frac{2{k}^{2}}{1+{k}^{2}}}$.
显然,若点H也在线段AB上,则由对称性可知,直线y=kx就是y轴,矛盾.
∵|AG|=|BH|,∴|AB|=|GH|.
∴$\sqrt{\frac{8(1+{k}^{2})}{1+2{k}^{2}}}$=2$\sqrt{\frac{7}{3}-\frac{2{k}^{2}}{1+{k}^{2}}}$,
解得k2=1,即k=±1.
点评 熟练掌握椭圆与圆的标准方程及其性质、直线与曲线相交问题转化为把直线l的方程与曲线的方程联立得到一元二次方程、利用根与系数的关系及弦长公式、垂径定理及半径、弦长的一半、弦心距三者之间的关系是解题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
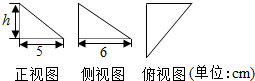
| A. | 25xcm2 | B. | $\frac{77π}{2}$cm2 | C. | 77πcm2 | D. | 144πcm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com