
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() ,连结
,连结![]() ,
,![]() 为
为![]() 的中点,则在翻折过程中,下列说法中所有正确的是( )
的中点,则在翻折过程中,下列说法中所有正确的是( )
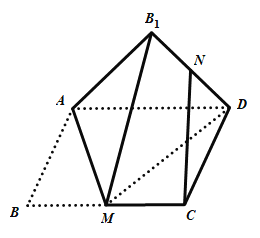
A.存在某个位置,使得![]()
B.翻折过程中,![]() 的长是定值
的长是定值
C.若![]() ,则
,则![]()
D.若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,三棱锥
的体积最大时,三棱锥![]() 的外接球的表面积是
的外接球的表面积是![]()
【答案】BD
【解析】
对于选项A,取![]() 中点
中点![]() ,取
,取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,通过假设
,通过假设![]() ,推出
,推出![]() 平面
平面![]() ,得到
,得到![]() ,则
,则![]() ,即可判断;
,即可判断;
对于选项B,在判断A的图基础上,连结![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,易得
,易得![]() ,由余弦定理,求得
,由余弦定理,求得![]() 为定值即可;
为定值即可;
对于选项C,取![]() 中点
中点![]() ,
,![]() ,
,![]() ,由线面平行的性质定理导出矛盾,即可判断;
,由线面平行的性质定理导出矛盾,即可判断;
对于选项D,易知当平面![]() 与平面
与平面![]() 垂直时,三棱锥
垂直时,三棱锥![]() 的体积最大,说明此时
的体积最大,说明此时![]() 中点
中点![]() 为外接球球心即可.
为外接球球心即可.
如图1,取![]() 中点
中点![]() ,取
,取![]() 中点
中点![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,
,
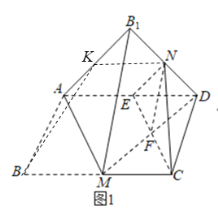
则易知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
由翻折可知,![]() ,
,![]() ,
,
对于选项A,易得![]() ,则
,则![]() 、
、![]() 、
、![]() 、
、![]() 四点共面,由题可知
四点共面,由题可知![]() ,若
,若![]() ,可得
,可得![]() 平面
平面![]() ,故
,故![]() ,则
,则![]() ,不可能,故A错误;
,不可能,故A错误;
对于选项B,易得![]() ,
,
在![]() 中,由余弦定理得
中,由余弦定理得![]() ,
,
整理得![]() ,
,
故![]() 为定值,故B正确;
为定值,故B正确;
如图2,取![]() 中点
中点![]() ,取
,取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,
,![]() ,,
,,
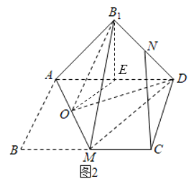
对于选项C,由![]() 得
得![]() ,若
,若![]() ,易得
,易得![]() 平面
平面![]() ,故有
,故有![]() ,从而
,从而![]() ,显然不可能,故C错误;
,显然不可能,故C错误;
对于选项D,由题易知当平面![]() 与平面
与平面![]() 垂直时,三棱锥B1﹣AMD的体积最大,此时
垂直时,三棱锥B1﹣AMD的体积最大,此时![]() 平面
平面![]() ,则
,则![]() ,由
,由![]() ,易求得
,易求得![]() ,
,![]() ,故
,故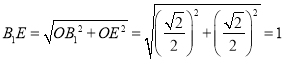 ,因此
,因此![]() ,
,![]() 为三棱锥
为三棱锥![]() 的外接球球心,此外接球半径为
的外接球球心,此外接球半径为![]() ,表面积为
,表面积为![]() ,故D正确.
,故D正确.
故选:BD.


科目:高中数学 来源: 题型:
【题目】(12分)若数列{an}是的递增等差数列,其中的a3=5,且a1,a2,a5成等比数列,
(1)求{an}的通项公式;
(2)设bn= ![]() ,求数列{bn}的前项的和Tn.
,求数列{bn}的前项的和Tn.
(3)是否存在自然数m,使得![]() <Tn<
<Tn<![]() 对一切n∈N*恒成立?若存在,求出m的值;
对一切n∈N*恒成立?若存在,求出m的值;
若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=6cos2![]() sinωx﹣3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形
sinωx﹣3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形
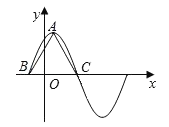
(1)求ω的值及函数f(x)的表达式;
(2)若f(x0)![]() ,且x0∈(
,且x0∈(![]() ),求f(x0+1)的值
),求f(x0+1)的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网购是现在比较流行的一种购物方式,现随机调查50名个人收入不同的消费者是否喜欢网购,调查结果表明:在喜欢网购的25人中有18人是低收入的人,另外7人是高收入的人,在不喜欢网购的25人中有6人是低收入的人,另外19人是高收入的人.
喜欢网购 | 不喜欢网购 | 总计 | |
低收入的人 | |||
高收入的人 | |||
总计 |
(Ⅰ)试根据以上数据完成![]() 列联表,并用独立性检验的思想,指出有多大把握认为是否喜欢网购与个人收入高低有关系;
列联表,并用独立性检验的思想,指出有多大把握认为是否喜欢网购与个人收入高低有关系;
(Ⅱ)将5名喜欢网购的消费者编号为1、2、3、4、5,将5名不喜欢网购的消费者编号也记作1、2、3、4、5,从这两组人中各任选一人进行交流,求被选出的2人的编号之和为2的倍数的概率.
参考公式:
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,
,![]() 是它的上顶点,点
是它的上顶点,点![]() 各不相同且均在椭圆上.
各不相同且均在椭圆上.
(1)若![]() 恰为椭圆长轴的两个端点,求
恰为椭圆长轴的两个端点,求![]() 的面积;
的面积;
(2)若![]() ,求证:直线
,求证:直线![]() 过一定点;
过一定点;
(3)若![]() ,
,![]() 的外接圆半径为
的外接圆半径为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 经过点
经过点![]() ,曲线
,曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(1)求曲线![]() 的普通方程,曲线
的普通方程,曲线![]() 的极坐标方程;
的极坐标方程;
(2)若![]() ,
,![]() 是曲线
是曲线![]() 上两点,当
上两点,当![]() 时,求
时,求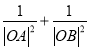 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一种掷骰子走跳棋的游戏:棋盘上标有第0站、第1站、第2站、…、第100站,共101站,设棋子跳到第n站的概率为![]() ,一枚棋子开始在第0站,棋手每掷一次骰子,棋子向前跳动一次.若掷出奇数点,棋子向前跳一站;若掷出偶数点,棋子向前跳两站,直到棋子跳到第99站(获胜)或第100站(失败)时,游戏结束(骰子是用一种均匀材料做成的立方体形状的游戏玩具,它的六个面分别标有点数1,2,3,4,5,6).
,一枚棋子开始在第0站,棋手每掷一次骰子,棋子向前跳动一次.若掷出奇数点,棋子向前跳一站;若掷出偶数点,棋子向前跳两站,直到棋子跳到第99站(获胜)或第100站(失败)时,游戏结束(骰子是用一种均匀材料做成的立方体形状的游戏玩具,它的六个面分别标有点数1,2,3,4,5,6).
(1)求![]() ,
,![]() ,
,![]() ,并根据棋子跳到第n站的情况,试用
,并根据棋子跳到第n站的情况,试用![]() 和
和![]() 表示
表示![]() ;
;
(2)求证:![]() 为等比数列;
为等比数列;
(3)求玩该游戏获胜的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com