
【题目】某公司生产一种产品每年需投入固定成本为3万元,此外每生产1百件这种产品还需要增加投入1万元(总成本![]() 固定成本
固定成本![]() 生产成本).已知销售收入满足函数:
生产成本).已知销售收入满足函数: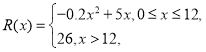 其中
其中![]() (百件)为年产量,假定该产品产销平衡(即生产的产品都能卖掉).
(百件)为年产量,假定该产品产销平衡(即生产的产品都能卖掉).
(1)请把年利润![]() 表示为当年生产量
表示为当年生产量![]() 的函数;(利润
的函数;(利润![]() 销售收入
销售收入![]() 总成本)
总成本)
(2)当年产量为多少百件时,公司所获利润最大?最大利润为多少?
科目:高中数学 来源: 题型:
【题目】变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5),变量U与V相对应的一组数据为 (10,5),(11.3,4),(11.8,3),(12.5,2),(13,1).r1表示变量Y与X之间的线性相关系数,r2表示变量V与U之间的线性相关系数,则( )
A.r2<r1<0 B.0<r2<r1
C.r2<0<r1 D.r2=r1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明中午放学回家自己煮面条吃,有下面几道工序:①洗锅盛水2分钟;②洗菜6分钟;③准备面条及佐料2分钟;④用锅把水烧开10分钟;⑤煮面条和菜共3分钟.以上各道工序,除了④之外,一次只能进行一道工序.小明要将面条煮好,最少要用( )
A. 13分钟 B. 14分钟
C. 15分钟 D. 23分钟
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人坐飞机去外地办一件急事,下面是他自己从家里出发到坐在机舱内这一过程的主要算法:
S1 乘车去飞机场售票处;
S2 _____;
S3 凭票上机,对号入座.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设平面直角坐标系原点与极坐标极点重合,x轴正半轴与极轴重合,若已知曲线C的极坐标方程为![]() ,点F1、F2为其左、右焦点,直线l的参数方程为
,点F1、F2为其左、右焦点,直线l的参数方程为 (t为参数,t∈R).
(t为参数,t∈R).
(Ⅰ)求曲线C的标准方程和直线l的普通方程;
(Ⅱ)若点P为曲线C上的动点,求点P到直线l的最大距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某加工厂用某原料由车间加工出 产品,由乙车间加工出 产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克 产品,每千克 产品获利40元.乙车间加工一箱原料需耗费工时6小时可加工出4千克 产品,每千克 产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工,每天甲、乙车间耗费工时总和不得超过480小时,甲、乙两车间每天获利最大的生产计划为( )
A. 甲车间加工原料10箱,乙车间加工原料60箱
B. 甲车间加工原料15箱,乙车间加工原料55箱
C. 甲车间加工原料18箱,乙车间加工原料50箱
D. 甲车间加工原料40箱,乙车间加工原料30箱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面五边形![]() 是轴对称图形(如图1),BC为对称轴,AD⊥CD,AD=AB=1,
是轴对称图形(如图1),BC为对称轴,AD⊥CD,AD=AB=1,![]() ,将此五边形沿BC折叠,使平面ABCD⊥平面BCEF,得到如图2所示的空间图形,对此空间图形解答下列问题.
,将此五边形沿BC折叠,使平面ABCD⊥平面BCEF,得到如图2所示的空间图形,对此空间图形解答下列问题.


(1)证明:AF∥平面DEC;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com