
【题目】科学家为研究对某病毒有效的疫苗,通过小鼠进行毒性和药效预实验.已知5只小鼠中有1只患有这种病毒引起的疾病,需要通过化验血液来确定患病的小鼠.血液化验结果呈阳性的即为患病小鼠,呈阴性即没患病.下面是两种化验方案:
方案甲:逐个化验,直到能确定患病小鼠为止.
方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病小鼠为止;若结果呈阴性则在另外2只中任取1只化验.
(1)求方案甲化验次数X的分布列;
(2)判断哪一个方案的效率更高,并说明理由.
科目:高中数学 来源: 题型:
【题目】某企业拟对某条生产线进行技术升级,现有两种方案可供选择:方案![]() 是报废原有生产线,重建一条新的生产线;方案
是报废原有生产线,重建一条新的生产线;方案![]() 是对原有生产线进行技术改造.由于受诸多不可控因素的影响,市场销售状态可能会发生变化.该企业管理者对历年产品销售市场行情及回报率进行了调研,编制出下表:
是对原有生产线进行技术改造.由于受诸多不可控因素的影响,市场销售状态可能会发生变化.该企业管理者对历年产品销售市场行情及回报率进行了调研,编制出下表:
市场销售状态 | 畅销 | 平销 | 滞销 | |
市场销售状态概率 |
|
|
| |
预期平均年利润(单位:万元) | 方案 | 700 | 400 |
|
方案 | 600 | 300 |
| |
(1)以预期平均年利润的期望值为决策依据,问:该企业应选择哪种方案?
(2)记该生产线升级后的产品(以下简称“新产品”)的年产量为![]() (万件),通过核算,实行方案
(万件),通过核算,实行方案![]() 时新产品的年度总成本
时新产品的年度总成本![]() (万元)为
(万元)为![]() ,实行方案
,实行方案时新产品的年度总成本
![]() (万元)为
(万元)为![]() .已知
.已知![]() ,
,![]() .若按(1)的标准选择方案,则市场行情为畅销、平销和滞销时,新产品的单价
.若按(1)的标准选择方案,则市场行情为畅销、平销和滞销时,新产品的单价![]() (元)分别为60,
(元)分别为60,![]() ,
,![]() ,且生产的新产品当年都能卖出去.试问:当
,且生产的新产品当年都能卖出去.试问:当![]() 取何值时,新产品年利润
取何值时,新产品年利润![]() 的期望取得最大值?并判断这一年利润能否达到预期目标.
的期望取得最大值?并判断这一年利润能否达到预期目标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,
中,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,点
的中点,点![]() 在对角线
在对角线![]() 上运动.当
上运动.当![]() 的面积取得最小值时,点
的面积取得最小值时,点![]() 的位置是( )
的位置是( )

A.线段![]() 的三等分点,且靠近点
的三等分点,且靠近点![]() B.线段
B.线段![]() 的中点
的中点
C.线段![]() 的三等分点,且靠近点
的三等分点,且靠近点![]() D.线段
D.线段![]() 的四等分点,且靠近点
的四等分点,且靠近点![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的部分图象如图所示,则下列叙述正确的是( )
的部分图象如图所示,则下列叙述正确的是( )
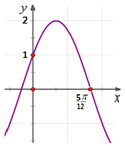
A.函数![]() 的图象可由
的图象可由![]() 的图象向左平移
的图象向左平移![]() 个单位得到
个单位得到
B.函数![]() 的图象关于直线
的图象关于直线![]() 对称
对称
C.函数![]() 在区间
在区间![]() 上是单调递增的
上是单调递增的
D.函数![]() 图象的对称中心为
图象的对称中心为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(1,0),动点M满足以MA为直径的圆与y轴相切.过A作直线x+(m﹣1)y+2m﹣5=0的垂线,垂足为B,则|MA|+|MB|的最小值为( )
A.2![]() B.2
B.2![]() C.
C.![]() D.3
D.3![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年春节期间,某服装超市举办了一次有奖促销活动,消费每超过600元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.
方案一:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,一次性摸出3个球,其中奖规则为:若摸到3个红球,享受免单优惠;若摸出2个红球则打6折,若摸出1个红球,则打7折;若没摸出红球,则不打折.
方案二:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
(1)若两个顾客均分别消费了600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某广告商租用了一块如图所示的半圆形封闭区域用于产品展示,该封闭区域由以![]() 为圆心的半圆及直径
为圆心的半圆及直径![]() 围成.在此区域内原有一个以
围成.在此区域内原有一个以![]() 为直径、
为直径、![]() 为圆心的半圆形展示区,该广告商欲在此基础上,将其改建成一个凸四边形的展示区
为圆心的半圆形展示区,该广告商欲在此基础上,将其改建成一个凸四边形的展示区![]() ,其中
,其中![]() 、
、![]() 分别在半圆
分别在半圆![]() 与半圆
与半圆![]() 的圆弧上,且
的圆弧上,且![]() 与半圆
与半圆![]() 相切于点
相切于点![]() .已知
.已知![]() 长为40米,设
长为40米,设![]() 为
为![]() .(上述图形均视作在同一平面内)
.(上述图形均视作在同一平面内)

(1)记四边形![]() 的周长为
的周长为![]() ,求
,求![]() 的表达式;
的表达式;
(2)要使改建成的展示区![]() 的面积最大,求
的面积最大,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com