
分析 求出两个命题是真命题时,m的范围,利用复合命题的真假,推出一真一假,然后求解即可.
解答 (8分)
解:若函数y=x2+mx+1在(-1,+∞)上单调递增,则-$\frac{m}{2}$≤-2,
∴m≥2,即p:m≥2. …(2分)
若函数y=-4x2+4(2-m)x-1≤0恒成立,
则△=16(m-2)2-16≤0,
解得1≤m≤3,即q:1≤m≤3 …(4分)
∵p∨q为真,p∧q为假,∴p、q一真一假
当p真q假时,由$\left\{\begin{array}{l}m≥2\\ m<1或m>3\end{array}\right.$解得:m>3 …(6分)
当p 假q真时,由$\left\{\begin{array}{l}m<2\\ 1≤m≤3\end{array}\right.$解得:1≤m<2
综上,m的取值范围是{m|m>3或1≤m<2}.…(8分)
点评 本题考查命题的真假的判断与应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | (-2,2] | C. | (-2,2) | D. | (-∞,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
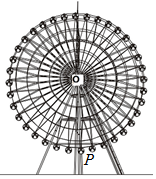 如图所示,游乐场中的摩天轮匀速逆时针旋转,每转一圈需要6min,其中心O距离地面40.5m,摩天轮的半径为40m,已知摩天轮上点P的起始位置在最低点处,在时刻t(min)时点P距离地面的高度为f(t)=Asin(ωt+φ)+h(A>0,ω>0,-π<φ<0,t≥0).
如图所示,游乐场中的摩天轮匀速逆时针旋转,每转一圈需要6min,其中心O距离地面40.5m,摩天轮的半径为40m,已知摩天轮上点P的起始位置在最低点处,在时刻t(min)时点P距离地面的高度为f(t)=Asin(ωt+φ)+h(A>0,ω>0,-π<φ<0,t≥0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com