
【题目】某工厂的固定成本为3万元,该工厂每生产100台某产品的生产成本为1万元,设生产该产品
![]() (百台),其总成本为
(百台),其总成本为![]() 万元(总成本=固定成本+生产成本),并且销售收入
万元(总成本=固定成本+生产成本),并且销售收入![]() 满足
满足![]() ,假设该产品产销平衡,根据上述统计数据规律求:
,假设该产品产销平衡,根据上述统计数据规律求:
(Ⅰ)要使工厂有盈利,产品数量![]() 应控制在什么范围?
应控制在什么范围?
(Ⅱ)工厂生产多少台产品时盈利最大?
【答案】(Ⅰ)![]() ;(Ⅱ)600.
;(Ⅱ)600.
【解析】
试题(Ⅰ)由于销售收入是一个关于产品数量x的一个分段函数,另外计算工厂的盈利需要将销售收入r(x)减去总的成本g(x)万元,所以在两段函数中分别求出盈利大于零的时候产品数量的范围,及可求得结论;(Ⅱ)通过二次函数的最值的求法即可得到盈利最大值时对应的产品数x的值,本小题单位的转化也是易错点.
试题解析:
解:依题意得![]() ,设利润函数为
,设利润函数为![]() ,则
,则![]() ,
,
所以 2分
2分
(Ⅰ)要使工厂有盈利,则有f(x)>0,因为
f(x)>0![]() , 4分
, 4分
![]()

![]() 或
或![]() , 6分
, 6分
即![]() . 7分
. 7分
所以要使工厂盈利,产品数量应控制在大于300台小于1050台的范围内. 8分
(Ⅱ)当![]() 时,
时, ![]()
故当x=6时,f(x)有最大值4.5. 10分
而当x>7时,![]() .
.
所以当工厂生产600台产品时,盈利最大. 12分


科目:高中数学 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了![]() 个网箱,测量各箱水产品的产量(单位:
个网箱,测量各箱水产品的产量(单位:![]() ),其频率分布直方图如下:
),其频率分布直方图如下:

(1)网箱产量不低于![]() 为“理想网箱”,填写下面列联表,并根据列联表判断是否有
为“理想网箱”,填写下面列联表,并根据列联表判断是否有![]() 的把握认为“理想网箱”的数目与养殖方法有关:
的把握认为“理想网箱”的数目与养殖方法有关:
箱产量 | 箱产量 | 合计 | |
旧养殖法 | |||
新养殖法 | |||
合计 |
(2)已知旧养殖法![]() 个网箱需要成本
个网箱需要成本![]() 元,新养殖法
元,新养殖法![]() 个网箱需要增加成本
个网箱需要增加成本![]() 元,该水产品的市场价格为
元,该水产品的市场价格为![]() 元/
元/![]() ,根据箱产量的频率分布直方图(说明:同一组中的数据用该组区间的中间值作代表),采用哪种养殖法,请给养殖户一个较好的建议,并说明理由.
,根据箱产量的频率分布直方图(说明:同一组中的数据用该组区间的中间值作代表),采用哪种养殖法,请给养殖户一个较好的建议,并说明理由.
附参考公式及参考数据:
|
|
|
|
|
|
|
|

查看答案和解析>>
科目:高中数学 来源: 题型:
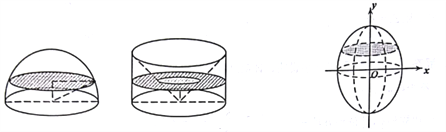
【题目】我国南北朝时间著名数学家祖暅提出了祖暅原理:“幂势既同,则积不容异”.意思是:夹在两平行平面间的两个几何体,被平行于这两个平行平面的任何平面所载,若截得的两个截面面积总相等,则这两个几何体的体积相等.为计算球的体积,构造一个底面半径和高都与球半径相等的圆柱,然后再圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,运用祖暅原理可证明此几何体与半球体积相等(任何一个平面所载的两个截面面积都相等).将椭圆![]() 绕
绕![]() 轴旋转一周后得一橄榄状的几何体,类比上述方法,运用祖暅原理可求得其体积等于( )
轴旋转一周后得一橄榄状的几何体,类比上述方法,运用祖暅原理可求得其体积等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱ABC-A1B1C1,侧面ABB1A1为菱形,侧面ACC1A1为正方形,侧面ABB1A1⊥侧面ACC1A1.
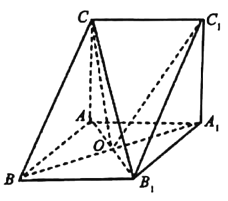
(1)求证:A1B⊥平面AB1C;
(2)若AB=2,∠ABB1=60°,求三棱锥C1-COB1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京101中学校园内有一个“少年湖”,湖的两侧有一个音乐教室和一个图书馆,如图,若设音乐教室在A处,图书馆在B处,为测量A,B两地之间的距离,某同学选定了与A,B不共线的C处,构成△ABC,以下是测量的数据的不同方案:①测量∠A,AC,BC;②测量∠A,∠B,BC;③测量∠C,AC,BC;④测量∠A,∠C,∠B. 其中一定能唯一确定A,B两地之间的距离的所有方案的序号是_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() 为棱
为棱![]() 的中点,
的中点,![]() 为棱
为棱![]() 上一点,
上一点,![]() .
.

(1)确定![]() 的位置,使得平面
的位置,使得平面![]()
![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(2)设二面角![]() 的正切值为
的正切值为![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点,且
上一点,且![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com