
分析 由函数f(x)=$\frac{1}{\root{3}{{x}^{2}+2x+1}+\root{3}{{x}^{2}-1}+\root{3}{{x}^{2}-2x+1}}$=$\frac{1}{2}$($\root{3}{x+1}$-$\root{3}{x-1}$),利用裂项相消法,可得答案.
解答 解:∵函数f(x)=$\frac{1}{\root{3}{{x}^{2}+2x+1}+\root{3}{{x}^{2}-1}+\root{3}{{x}^{2}-2x+1}}$=$\frac{\root{3}{x+1}-\root{3}{x-1}}{(\root{3}{x+1}-\root{3}{x-1})(\root{3}{{x}^{2}+2x+1}+\root{3}{{x}^{2}-1}+\root{3}{{x}^{2}-2x+1})}$=$\frac{\root{3}{x+1}-\root{3}{x-1}}{{\root{3}{x+1}}^{3}-{\root{3}{x-1}}^{3}}$=$\frac{\root{3}{x+1}-\root{3}{x-1}}{x+1-{(x-1)}^{\;}}$=$\frac{1}{2}$($\root{3}{x+1}$-$\root{3}{x-1}$),
∴f(1)+f(3)+f(5)+…+f(2k-1)+…+f(999)=$\frac{1}{2}$($\root{3}{2}$-0)+$\frac{1}{2}$($\root{3}{4}$-$\root{3}{2}$)+$\frac{1}{2}$($\root{3}{6}$-$\root{3}{4}$)+…+$\frac{1}{2}$($\root{3}{1000}$-$\root{3}{998}$)=$\frac{1}{2}$$\root{3}{1000}$=5.
点评 本题考查的知识点是函数求值,其中利用立方差公式,将函数解析式化为:f(x)=$\frac{1}{2}$($\root{3}{x+1}$-$\root{3}{x-1}$),是解答的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 0 | C. | -1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∧(-q)是真命题 | D. | 命题p∨(-q)是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 当n=5时该命题不成立 | B. | 当n=5时该命题成立 | ||
| C. | 当n=2时该命题不成立 | D. | 当n=2时该命题成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
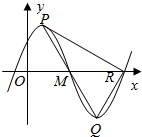 如图是函数f(x)=Asin(ωx+φ)的部分图象,P、Q分别为该图象的最高点和最低点,R是该图象与x轴的一个交点,且PR⊥QR,△PQR的面积为2$\sqrt{3}$,则函数f(x)的最小正周期为4.
如图是函数f(x)=Asin(ωx+φ)的部分图象,P、Q分别为该图象的最高点和最低点,R是该图象与x轴的一个交点,且PR⊥QR,△PQR的面积为2$\sqrt{3}$,则函数f(x)的最小正周期为4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com