
【题目】已知正项等比数列{an}前n项和为Sn , 且满足S3= ![]() ,a6 , 3a5 , a7成等差数列. (Ⅰ)求数列{an}的通项公式;
,a6 , 3a5 , a7成等差数列. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列bn= ![]() ,且数列bn的前n项的和Tn , 试比较Tn与
,且数列bn的前n项的和Tn , 试比较Tn与 ![]() 的大小.
的大小.
【答案】解:(Ⅰ)设等比数列的公比为q, 因为a6 , 3a5 , a7成等差数列,
所以6a5=a6+a7 ,
所以6a5=qa5+q2a5 .
因为a5≠0,
所以q2+q﹣6=0,
又an>0,
所以q=2.
由S3= ![]() ,
,
解得a1= ![]() ,
,
所以通项公式为an= ![]() 2n﹣1=2n﹣2 .
2n﹣1=2n﹣2 .
(Ⅱ)bn= ![]()
= ![]()
= ![]()
= ![]()
= ![]() (
( ![]() ﹣
﹣ ![]() )
)
所以Tn=b1+b2+b3+…+bn
= ![]() (1﹣
(1﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() )
)
= ![]() (1﹣
(1﹣ ![]() )<
)< ![]()
【解析】(Ⅰ)根据等差数列和等比数列的性质即可求出公比,问题得以解决;(Ⅱ)根据对数的运算性质和裂项求和以及放缩法即可求出答案.
【考点精析】掌握等比数列的通项公式(及其变式)和数列的前n项和是解答本题的根本,需要知道通项公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系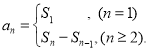 .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】已知![]() (
(![]() ).
).
(1)当![]() 时,求关于
时,求关于![]() 的不等式
的不等式![]() 的解集;
的解集;
(2)若f(x)是偶函数,求k的值;
(3)在(2)条件下,设![]() ,若函数
,若函数![]() 与
与![]() 的图象有公共点,求实数b的取值范围.
的图象有公共点,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() ,
,![]() 为两个不同的平面,
为两个不同的平面,![]() ,
,![]() 为两条不同的直线,下列命题中正确的是( )
为两条不同的直线,下列命题中正确的是( )
①若![]() ,
,![]() ,则
,则![]() ; ②若
; ②若![]() ,
,![]() ,则
,则![]() ;
;
③若![]() ,
,![]() ,
,![]() ,则
,则![]() ④若
④若![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在圆x2+y2﹣4x+2y=0内,过点E(1,0)的最长弦和最短弦分别是AC和BD,则四边形ABCD的面积为( )
A.![]()
B.6 ![]()
C.![]()
D.2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,且过定点M(1,
,且过定点M(1, ![]() ).
).
(1)求椭圆C的方程;
(2)已知直线l:y=kx﹣ ![]() (k∈R)与椭圆C交于A、B两点,试问在y轴上是否存在定点P,使得以弦AB为直径的圆恒过P点?若存在,求出P点的坐标和△PAB的面积的最大值,若不存在,说明理由.
(k∈R)与椭圆C交于A、B两点,试问在y轴上是否存在定点P,使得以弦AB为直径的圆恒过P点?若存在,求出P点的坐标和△PAB的面积的最大值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,直线l的参数方程 ![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,已知曲线C的极坐标方程为p2cos2θ+p2sinθ﹣2psinθ﹣3=0
(t为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,已知曲线C的极坐标方程为p2cos2θ+p2sinθ﹣2psinθ﹣3=0
(1)求直线l的极坐标方程;
(2)若直线l与曲线C相交于A,B两点,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为r米,高为h米,体积为V立方米.假设建造成本仅与表面积有关,侧面的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12 000π元(π为圆周率).
(1)将V表示成r的函数V(r),并求该函数的定义域;
(2)讨论函数V(r)的单调性,并确定r和h为何值时该蓄水池的体积最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com