
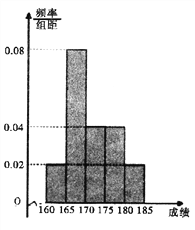
【题目】近期中央电视台播出的《中国诗词大会》火遍全国.某选拔赛后,随机抽取100名选手的成绩,按成绩由低到高依次分为第1,2,3,4,5组,制成频率分布直方图如下图所示:
(I)在第3、4、5组中用分层抽样抽取5名选手,求第3、4、5组每组各抽取多少名选手;
(II)在(I)的前提下,在5名选手中随机抽取2名选手,求第4组至少有一名选手被抽取的概率.
【答案】(I)2人、2人、1人;(II)![]() .
.
【解析】试题分析:(I)根据频率分布直方图可以求出3、4、5组的频数分别为20、20、10,根据分层抽样的原则:比例相同,可以得到抽取的人数:3组2人;4组2人;5组1人;(Ⅱ)根据古典概型分别列举出从五位选手中抽取两位选手的总事件有10种,其中第4组至少有一名选手的事件有7,故概率为![]() .
.
试题解析:(I)由频率分布直方图易知第3组的频率为![]() ,从而第3组的频数为
,从而第3组的频数为![]() ,同理可得第4、5组的频数分别为20、10,所以第3、4、5组共有50名选手.
,同理可得第4、5组的频数分别为20、10,所以第3、4、5组共有50名选手.
利用分层抽样在50名选手中抽取5名选手,每组抽取的人数分别为:
第3组: ![]() 人,第4组:
人,第4组: ![]() 人,第5组:
人,第5组: ![]() 人,
人,
所以第3、4、5组分别抽取2人、2人、1人.
(Ⅱ)设第3组的2位选手为![]() ,
, ![]() ,第4组的2位选手为
,第4组的2位选手为![]() ,
, ![]() ,第5组的1位选手为
,第5组的1位选手为![]() ,则从这五位选手中抽取两位选手有
,则从这五位选手中抽取两位选手有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,共10种.其中第4组的2位选手
,共10种.其中第4组的2位选手![]() ,
, ![]() 中至少有一位选手入选的有:
中至少有一位选手入选的有: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,共有7种,所以第4组至少有一名选手的概率为
,共有7种,所以第4组至少有一名选手的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣1|﹣x,
(1)用分段函数的形式表示该函数,并画出该函数的图象;
(2)写出该函数的值域、单调区间(不要求证明);
(3)若对任意x∈R,不等式|2x﹣1|≥a+x恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,定义椭圆
,定义椭圆![]() 上的点
上的点![]() 的“伴随点”为
的“伴随点”为![]() .
.
(1)求椭圆![]() 上的点
上的点![]() 的“伴随点”
的“伴随点”![]() 的轨迹方程;
的轨迹方程;
(2)如果椭圆![]() 上的点
上的点![]() 的“伴随点”为
的“伴随点”为![]() ,对于椭圆
,对于椭圆![]() 上的任意点
上的任意点![]() 及它的“伴随点”
及它的“伴随点”![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)当![]() ,
, ![]() 时,直线
时,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,若点
两点,若点![]() ,
, ![]() 的“伴随点”分别是
的“伴随点”分别是![]() ,
, ![]() ,且以
,且以![]() 为直径的圆经过坐标原点
为直径的圆经过坐标原点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
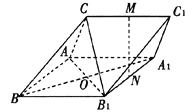
【题目】如图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.
(I)证明:直线MN//平面CAB1;
(II)BA=BC=BB1,CA=CB1,CA⊥CB1,∠ABB1=60°,求平面AB1C和平面A1B1C1所成的角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家拟在2017年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)![]() (单位:万件)与年促销费用
(单位:万件)与年促销费用![]() (单位:万元)(
(单位:万元)(![]() )满足
)满足![]() (
(![]() 为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2017年生产该产品的固定投入为8万元.每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2017年生产该产品的固定投入为8万元.每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2017年该产品的利润![]() (单位:万元)表示为年促销费用
(单位:万元)表示为年促销费用![]() (单位:万元)的函数;
(单位:万元)的函数;
(2)该厂家2017年的促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知⊙![]() :
: ![]() 与⊙
与⊙![]() :
: ![]() ,以
,以![]() ,
, ![]() 分别为左右焦点的椭圆
分别为左右焦点的椭圆![]() :
: ![]() 经过两圆的交点。
经过两圆的交点。
(Ⅰ)求椭圆![]() 的方程;
的方程;
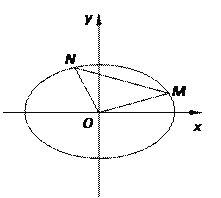
(Ⅱ)![]() 、
、![]() 是椭圆
是椭圆![]() 上的两点,若直线
上的两点,若直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() ,试问
,试问![]() 的面积是否为定值?若是,求出这个定值;若不是,请说明理由。
的面积是否为定值?若是,求出这个定值;若不是,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|﹣1≤x≤10},集合B={x|2x﹣6≥0}.
求R(A∪B);
已知C={x|a<x<a+1},且CA,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com