
【题目】设椭圆 ![]() +
+ ![]() =1(a>b>0)的左、右焦点分别为F1、F2 , P是椭圆上一点,|PF1|=λ|PF2|(
=1(a>b>0)的左、右焦点分别为F1、F2 , P是椭圆上一点,|PF1|=λ|PF2|( ![]() ≤λ≤2),∠F1PF2=
≤λ≤2),∠F1PF2= ![]() ,则椭圆离心率的取值范围为( )
,则椭圆离心率的取值范围为( )
A.(0, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,1)
,1)
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)对任意的x都有f(x+2)﹣f(x)=﹣4x+4,且f(0)=0.
(1)求函数f(x)的解析式;
(2)设函数g(x)=f(x)+m,(m∈R). ①若存在实数a,b(a<b),使得g(x)在区间[a,b]上为单调函数,且g(x)取值范围也为[a,b],求m的取值范围;
②若函数g(x)的零点都是函数h(x)=f(f(x))+m的零点,求h(x)的所有零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=( ![]() )x﹣2x .
)x﹣2x .
(1)若f(x)= ![]() ,求x的值;
,求x的值;
(2)若不等式f(2m﹣mcosθ)+f(﹣1﹣cosθ)<f(0)对所有θ∈[0, ![]() ]都成立,求实数m的取值范围.
]都成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中a是0﹣9的某个整数 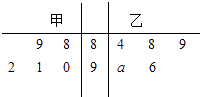
(1)若该厂决定从甲乙两人中选派一人去参加技能培训,从成绩稳定性角度考虑,你认为谁去比较合适?
(2)若从甲的成绩中任取两次成绩作进一步分析,在抽取的两次成绩中,求至少有一次成绩在(90,100]之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P是圆F1:(x+1)2+y2=16上任意一点(F1是圆心),点F2与点F1关于原点对称.线段PF2的中垂线m分别与PF1、PF2交于M、N两点.
(1)求点M的轨迹C的方程;
(2)直线l经过F2 , 与抛物线y2=4x交于A1 , A2两点,与C交于B1 , B2两点.当以B1B2为直径的圆经过F1时,求|A1A2|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,角A、B、C的对边分别为a、b、c.已知(a+c)2﹣b2=3ac
(1)求角B;
(2)当b=6,sinC=2sinA时,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线C上的动点M到定点F(1,0)的距离和它到定直线x=3的距离之比是1: ![]() .
.
(1)求曲线C的方程;
(2)过点F(1,0)的直线l与C交于A,B两点,当△ABO面积为 ![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}是公差d不为0的等差数列,a1=2,Sn为其前n项和.
(1)当a3=6时,若a1 , a3 , ![]() ,
, ![]() …,
…, ![]() 成等比数列(其中3<n1<n2<…<nk),求nk的表达式;
成等比数列(其中3<n1<n2<…<nk),求nk的表达式;
(2)是否存在合适的公差d,使得{an}的任意前3n项中,前n项的和与后n项的和的比值等于定常数?求出d,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com