已知函数f(x)=2x-sinx,若对任意的t∈[-3,1],f(tx-3)+f(2x)<0恒成立,则实数x的取值范围是________.
(-3,1)
分析:由题意可知f(x)=2x-sinx为奇函数,由f′(x)=2-cosx>0可判断其单调性,从而可求对任意的t∈[-3,1],f(tx-3)+f(2x)<0恒成立时实数x的取值范围.
解答:解;∵f(-x)=-2x-sin(-x)=-(2x-sinx)=-f(x),
∴f(x)=2x-sinx为奇函数;
又f′(x)=2-cosx>0,
∴f(x)=2x-sinx为R上的增函数.
∴对任意的t∈[-3,1],f(tx-3)+f(2x)<0恒成立
?对任意的t∈[-3,1],f(tx-3)<f(-2x)恒成立
?tx-3<-2x恒成立,t∈[-3,1]
?tx+2x-3<0恒成立,t∈[-3,1].
令g(t)=tx+2x-3,则
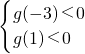
,即
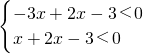
,
解得:-3<x<1.
∴实数x的取值范围是(-3,1).
故答案为:(-3,1).
点评:本题考查函数恒成立问题,考查函数的奇偶性与单调性,突出转化思想与构造函数思想的综合应用,属于中档题.

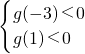 ,即
,即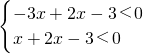 ,
,

 阅读快车系列答案
阅读快车系列答案