
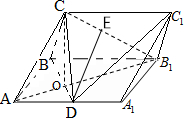
 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=$\sqrt{2}$,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1,E为线段B1C的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=$\sqrt{2}$,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1,E为线段B1C的中点.分析 (Ⅰ)取BC的中点F,连接AF,EF,则EF平行且等于AD,证明:ADEF是平行四边形,可得AF∥DE,即可证明DE∥平面ABC;
(Ⅱ)作OM⊥AB,连接CM,则CM⊥AB,∠CMO为二面角C-AB-A1的平面角,即可求二面角C-AB-A1的余弦值.
解答  (Ⅰ)证明:取BC的中点F,连接AF,EF,则EF平行且等于AD,
(Ⅰ)证明:取BC的中点F,连接AF,EF,则EF平行且等于AD,
∴ADEF是平行四边形,
∴AF∥DE,
∵DE?平面ABC,AF?平面ABC,
∴DE∥平面ABC;
(Ⅱ)解:作OM⊥AB,连接CM,则CM⊥AB,∠CMO为二面角C-AB-A1的平面角,
侧面ABB1A1为矩形,AB=1,AA1=$\sqrt{2}$,∴AO=$\frac{\sqrt{3}}{3}$=CO,OM=$\frac{\sqrt{2}}{3}$
∴CM=$\frac{\sqrt{5}}{3}$,
∴二面角C-AB-A1的余弦值=$\frac{\sqrt{10}}{5}$.
点评 本题考查线面平行的判定,考查二面角的余弦值,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源:2015-2016学年江西省南昌市高二理下学期期末考试数学试卷(解析版) 题型:选择题
如果小明在某一周的第一天和第七天分别吃了3个水果,且从这周的第二天开始,每天所吃水果的个数与前一天相比,仅存在三种可能:或“多一个”或“持平”或“少一个”,那么小明在这一周中每天所吃水果个数的不同选择方案共有( )种
A.50 B.51 C.140 D.141
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com