
【题目】如图,在五面体ABCDPN中,棱PA⊥面ABCD,AB=AP=2PN,底面ABCD是菱形,∠BAD=![]() .
.

(1)求证:PN∥AB;
(2)求NC与平面BDN所成角的正弦值.
【答案】(1)见解析; (2)![]() .
.
【解析】
(1)菱形得线线平行,进而得线面平行,再得线线平行;
(2)需建立空间坐标系,找出相关点的坐标,利用公式计算得解.
(1)证明:
在菱形ABCD中,AB∥CD
∵CD面CDPN,AB面CDPN
∴AB∥面CDPN
又面ABNP∩面CDPN=PN
∴AB∥PN
(2)取CD中点M,
在菱形ABCD中,∠BAD=![]() ,可知AM⊥AB
,可知AM⊥AB
又PA⊥面ABCD
∴以A为原点建立空间坐标系如图
设AB=2,则B(2,0,0)
N(1,0,2),D(﹣1,![]() ,0),C(1,
,0),C(1,![]() ,0)
,0)
∴![]() =(0,
=(0,![]() ,﹣2)
,﹣2)
![]() =(1,0,﹣2)
=(1,0,﹣2)
![]() =(﹣3,
=(﹣3,![]() ,0)
,0)
设面BDN的法向量为![]() =(m,n,p)
=(m,n,p)
则![]() ,得
,得![]()
取m=2,则n=2![]() ,p=1
,p=1
即![]() =(2,2
=(2,2![]() ,1)
,1)
设NC与平面BDN所成的角为θ,
则sinθ=|cos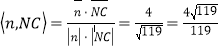 ,
,
故NC与平面BDN所成角的正弦值为![]() .
.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
【题目】已知F1 , F2是双曲线C1: ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左、右焦点,且F2是抛物线C2:y2=2px(p>0)的焦点,P是双曲线C1与抛物线C2在第一象限内的交点,线段PF2的中点为M,且|OM|=
=1(a>0,b>0)的左、右焦点,且F2是抛物线C2:y2=2px(p>0)的焦点,P是双曲线C1与抛物线C2在第一象限内的交点,线段PF2的中点为M,且|OM|= ![]() |F1F2|,其中O为坐标原点,则双曲线C1的离心率是( )
|F1F2|,其中O为坐标原点,则双曲线C1的离心率是( )
A.2+ ![]()
B.1+ ![]()
C.2+ ![]()
D.1+ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三次函数f(x)=x3+bx2+cx+d(a,b,c∈R)过点(3,0),且函数f(x)在点(0,f(0))处的切线恰好是直线y=0.
(1)求函数f(x)的解析式;
(2)设函数g(x)=9x+m﹣1,若函数y=f(x)﹣g(x)在区间[﹣2,1]上有两个零点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某零售店近5个月的销售额和利润额资料如下表:
商店名称 |
|
|
|
|
|
销售额 | 3 | 5 | 6 | 7 | 9 |
利润额 | 2 | 3 | 3 | 4 | 5 |
(1)画出散点图.观察散点图,说明两个变量有怎样的相关关系;
(2)用最小二乘法计算利润额![]() 关于销售额
关于销售额![]() 的回归直线方程;
的回归直线方程;
(3)当销售额为4千万元时,利用(2)的结论估计该零售店的利润额(百万元).
[参考公式: ,
,![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一网站营销部为统计某市网友2017年12月12日在某网店的网购情况,随机抽查了该市60名网友在该网店的网购金额情况,如下表:
网购金额(单位:千元) | 频数 | 频率 | 网购金额(单位:千元) | 频数 | 频率 | |
[0,0.5) | 3 | 0.05 | [1.5,2) | 15 | 0.25 | |
[0.5,1) |
|
| [2,2.5) | 18 | 0.30 | |
[1,1.5) | 9 | 0.15 | [2.5,3] |
|
|
若将当日网购金额不小于2千元的网友称为“网购达人”,网购金额小于2千元的网友称为“网购探者”,已知“网购达人”与“网购探者”人数的比例为2:3.
(1)确定![]() ,
,![]() ,
,![]() ,
,![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;

(2)①.试根据频率分布直方图估算这60名网友当日在该网店网购金额的平均数和中位数;
②.若平均数和中位数至少有一个不低于2千元,则该网店当日评为“皇冠店”,试判断该网店当日能否被评为“皇冠店”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标![]() 中,圆
中,圆![]() ,圆
,圆![]() 。
。
(Ⅰ)在以O为极点,x轴正半轴为极轴的极坐标系中,分别写出圆![]() 的极坐标方程,并求出圆
的极坐标方程,并求出圆![]() 的交点坐标(用极坐标表示);
的交点坐标(用极坐标表示);
(Ⅱ)求圆![]() 的公共弦的参数方程。
的公共弦的参数方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,直线x+y+
,直线x+y+ ![]() =0与椭圆E仅有一个公共点.
=0与椭圆E仅有一个公共点.
(1)求椭圆E的方程;
(2)直线l被圆O:x2+y2=3所截得的弦长为3,且与椭圆E交于A、B两点,求△ABO面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右顶点分别为
的左右顶点分别为![]() ,左焦点为
,左焦点为![]() ,已知椭圆
,已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若过点![]() 的直线与该椭圆
的直线与该椭圆![]() 交于
交于![]() 两点,且线段
两点,且线段![]() 的中点恰为点
的中点恰为点![]() ,且直线
,且直线![]() 的方程;
的方程;
(3)若经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,记
两点,记![]() 与
与![]() 的面积分别为
的面积分别为![]() 和
和![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com