练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在△ABC中，AC=6， ， ．
    （1）求AB的长；
    （2）求 的值．

    【答案】
    （1）解：因为 ，0＜B＜π，

    所以 = ．

    由正弦定理知 ，

    所以


    （2）解：在△ABC中，A+B+C=π，

    所以A=π﹣（B+C），

    于是 = ，

    又 ， ，

    故 ．

    因为0＜A＜π，

    所以 ．

    因此， =


    【解析】（1）由同角的三角函数关系得出sinB的值，再根据正弦定理解出AB的大小，（2）在△ABC中，A+B+C=π，cosA=-cos（B+C），即可解得cosA的值，根据同角三角函数关系得出sinA的值，由两角差的余弦公式展开，代值即可得出答案.
    【考点精析】本题主要考查了正弦定理的定义的相关知识点，需要掌握正弦定理:才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，过椭圆C： 的左顶点A作直线l，与椭圆C和y轴正半轴分别交于点P，Q．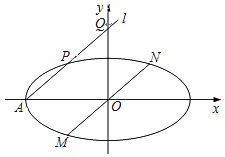

    （1）若AP=PQ，求直线l的斜率；
    （2）过原点O作直线l的平行线，与椭圆C交于点M，N，求证： 为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=lnx﹣x， ．
    （1）求h（x）的最大值；
    （2）若关于x的不等式xf（x）≥﹣2x2+ax﹣12对一切x∈（0，+∞）恒成立，求实数a的取值范围；
    （3）若关于x的方程f（x）﹣x3+2ex2﹣bx=0恰有一解，其中e是自然对数的底数，求实数b的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】以下四个关于圆锥曲线的命题中：
    ①双曲线 与椭圆 有相同的焦点；
    ②以抛物线的焦点弦（过焦点的直线截抛物线所得的线段）为直径的圆与抛物线的准线是相切的；
    ③设A，B为两个定点，k为常数，若|PA|﹣|PB|=k，则动点P的轨迹为双曲线；
    ④过定圆C上一点A作圆的动弦AB，O为原点，若 则动点P的轨迹为椭圆．其中正确的个数是（ ）
    A.1个
    B.2个
    C.3个
    D.4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数y=f（x）图象上不同的两点M（x1 ， y1），N（x2 ， y2）处的切线斜率分别是kM ， kN ， 那么规定Φ（M，N）= 叫做曲线y=f（x）在点M与点N之间的“弯曲度”．设曲线f（x）=x3+2上不同两点M（x1 ， y1），N（x2 ， y2），且x1x2=1，则该曲线在点M与点N之间的“弯曲度”的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列四个命题：①f（x）=sin（2x﹣ ）的对称轴为x= ，k∈Z；②若函数y=2cos（ax﹣ ）（a＞0）的最小正周期是π，则a=2；③函数f（x）=sinxcosx﹣1的最小值为﹣ ；④函数y=sin（x+ ）在[﹣ ]上是增函数，其中正确命题的个数是（ ）
    A.1个
    B.2个
    C.3个
    D.4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x﹣alnx（a∈R）
    （1）当a=2时，求曲线y=f（x）在点A（1，f（1））处的切线方程．
    （2）求函数f（x）的极值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设数列{an}是各项均为正数的等比数列，其前n项和为Sn ， 若a1a5=64，S5﹣S3=48．
    （1）求数列{an}的通项公式；
    （2）对于正整数k，m，l（k＜m＜l），求证：“m=k+1且l=k+3”是“5ak ， am ， al这三项经适当排序后能构成等差数列”成立的充要条件；
    （3）设数列{bn}满足：对任意的正整数n，都有a1bn+a2bn﹣1+a3bn﹣2+…+anb1=32n+1﹣4n﹣6，且集合 中有且仅有3个元素，试求λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量 ， ，设 ．
    （Ⅰ）若f（α）=2，求 的值；
    （Ⅱ）在△ABC中，角A，B，C的对边分别是a，b，c，且满足（2a﹣b）cosC=ccosB，求f（A）的取值范围．

    查看答案和解析>>

    同步练习册答案