Question

在三棱锥P-ABC中，△PAC和△PBC是边长为

2

的等边三角形，AB=2，O是AB中点．
（1）在棱PA上求一点M，使得OM∥平面PBC；
（2）求证：平面PAB⊥平面ABC；
（3）求二面角P-BC-A的余弦值．

Answer 1

分析：（1）当M为棱PA中点时，证明平面PBC内的直线PB与平面外的中心OM平行，即可证明OM∥平面PBC；
（2）连接OC，OP，要证平面PAB⊥平面ABC只需证明，平面PAB内的直线PO垂直平面ABC，即可；
（3）建立空间直角坐标系，求出平面PBC的法向量和平面ABC的一个法向量，利用二者的数量积求二面角P-BC-A的余弦值．

解答：解：（Ⅰ）当M为棱PA中点时，OM∥平面PBC．
证明如下：∵M，O分别为PA，AB中点，∴OM∥PB
又PB?平面PBC，OM?平面PBC∴OM∥平面PBC．（4分）
（Ⅱ）连接OC，OP
∵AC=CB=

2

，O为AB中点，AB=2，
∴OC⊥AB，OC=1．
同理，PO⊥AB，PO=1．
又PC=

2

，
∴PC²=OC²+PO²=2，∴∠POC=90°．∴PO⊥OC．
∵PO⊥OC，PO⊥AB，AB∩OC=O，
∴PO⊥平面ABC．
∵PO?平面PAB，
∴平面PAB⊥平面ABC．（9分）

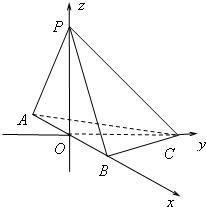
（Ⅲ）如图，建立空间直角坐标系O-xyz．
则B（1，0，0），C（0，1，0），P（0，0，1），
∴

BC

=(-1，1，0)，

PB

=(1，0，-1)．
由（Ⅱ）知

OP

=(0，0，1)是平面ABC的一个法向量．
设平面PBC的法向量为n=（x，y，z），
则

n• BC =0 n• PB =0

?

-x+y=0 x-z=0

．
令z=1，则x=1，y=1，
∴平面PBC的一个法向量n=（1，1，1）．
∴cos＜

OP

，n＞=

OP •n

| OP |•|n|

=

1

1× 3

=

3

3

．
∵二面角P-BC-A的平面角为锐角，
∴所求二面角P-BC-A的余弦值为

3

3

．（14分）

点评：本题考查平面与平面垂直的判定，直线与平面的平行，二面角的求法，考查空间想象能力 逻辑思维能力，是中档题．