
直线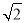 ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( ).
ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( ).
A.0 B. C.
C. -1 D.
-1 D. +1
+1
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练8练习卷(解析版) 题型:解答题
已知△ABC的内角A,B,C所对的边分别是a,b,c,设向量m=(a,b),n=(sin B,sin A),p=(b-2,a-2).
(1)若m∥n,求证:△ABC为等腰三角形;
(2)若m⊥p,边长c=2,C= ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练17练习卷(解析版) 题型:选择题
某学校有男、女学生各500名,为了解男、女学生在学习兴趣与业余爱好方面是否存在显著差异,拟从全体学生中抽取100名学生进行调查,则宜采用的抽样方法是( ).
A.抽签法 B.随机数法 C.系统抽样法 D.分层抽样法
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(解析版) 题型:解答题
在平面直角坐标系xOy中,曲线y=x2-6x+1与坐标轴的交点都在圆C上.
(1)求圆C的方程;
(2)若圆C与直线x-y+a=0交于A,B两点,且OA⊥OB,求a的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练13练习卷(解析版) 题型:解答题
如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.

(1)证明B1C1⊥CE;
(2)求二面角B1-CE-C1的正弦值;
(3)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为 ,求线段AM的长.
,求线段AM的长.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练13练习卷(解析版) 题型:选择题
已知正三棱柱ABC-A1B1C1的侧棱长与底面边长相等,则AB1与侧面ACC1A1所成角的正弦等于( ).

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练11练习卷(解析版) 题型:解答题
已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形.

(1)求该几何体的体积V;
(2)求该几何体的侧面积S.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷4练习卷(解析版) 题型:解答题
如图所示为一个几何体的直观图、三视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形).

(1)求四棱锥P-ABCD的体积;
(2)若G为BC上的动点,求证:AE⊥PG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com