
【题目】已知数列{an}中,a1=1,an>0,前n项和为Sn,若![]() (n∈N*,且n≥2).
(n∈N*,且n≥2).
(1)求数列{an}的通项公式;
(2)记![]() ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
【答案】(1) an=2n﹣1;(2) Tn![]() .
.
【解析】
(1)根据题意,有an=Sn﹣Sn﹣1,结合![]() 分析可得
分析可得![]() 1,则数列{
1,则数列{![]() }是以
}是以![]() 1为首项,公差为1的等差数列,由等差数列的通项公式可得
1为首项,公差为1的等差数列,由等差数列的通项公式可得![]() 1+(n﹣1)=n,则Sn=n2,据此分析可得答案;
1+(n﹣1)=n,则Sn=n2,据此分析可得答案;
(2)由(1)的结论可得cn=(2n﹣1)×22n﹣1;进而可得Tn=1×2+3×23+5×25+……+(2n﹣1)×22n﹣1,由错位相减法分析可得答案.
(1)数列{an}中,an=Sn﹣Sn﹣1,(n∈N*,且n≥2)①
![]() ,(n∈N*,且n≥2)②
,(n∈N*,且n≥2)②
①÷②可得:![]() 1,
1,
则数列{![]() }是以
}是以![]() 1为首项,公差为1的等差数列,
1为首项,公差为1的等差数列,
则![]() 1+(n﹣1)=n,
1+(n﹣1)=n,
则Sn=n2,
当n=1时,a1=S1=1,
当n≥2时,an=Sn﹣Sn﹣1=2n﹣1,
a1=1也符合该式,
则an=2n﹣1;
(2)有(1)的结论,an=2n﹣1,
则cn=(2n﹣1)×22n﹣1;
则Tn=1×2+3×23+5×25+……+(2n﹣1)×22n﹣1,③;
则4Tn=1×23+3×25+5×27+……+(2n﹣1)×22n+1,④;
③﹣④可得:﹣3Tn=2+2(23+25+……+22n﹣1)﹣(2n﹣1)×22n+1![]() (
(![]() 2n)×22n+1,
2n)×22n+1,
变形可得:Tn![]() .
.


科目:高中数学 来源: 题型:
【题目】北京联合张家口获得2022年第24届冬奥会举办权,我国各地掀起了发展冰雪运动的热潮,现对某高中的学生对于冰雪运动是否感兴趣进行调查,该高中男生人数是女生的1.2倍,按照分层抽样的方法,从中抽取110人,调查高中生“是否对冰雪运动感兴趣”得到如下列联表:
感兴趣 | 不感兴趣 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 | 110 |
(1)补充完成上述![]() 列联表;
列联表;
(2)是否有99%的把握认为是否喜爱冰雪运动与性别有关.
附:![]() (其中
(其中![]() ).
).
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体ABCD﹣A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线E,F的平面分别与棱BB′、DD′交于M,N,设BM=x,x∈[0,1],给出以下四个命题:
①平面MENF⊥平面BDD′B′;
②当且仅当x=![]() 时,四边形MENF的面积最小;
时,四边形MENF的面积最小;
③四边形MENF周长L=f(x),x∈[0,1]是单调函数;
④四棱锥C′﹣MENF的体积V=h(x)为常函数;
以上命题中假命题的序号为( )
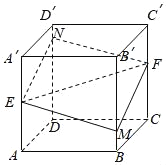
A. ①④B. ②C. ③D. ③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学习小组在生物研究性学习中,对春季昼夜温差大小与黄豆种子发芽多少之间的关系进行研究,于是小组成员在3月份的31天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下资料:
日期 | 3月2日 | 3月8日 | 3月15日 | 3月22日 | 3月28日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 14 |
(1)在这个学习小组中负责统计数据的那位同学为了减少计算量,他从这5天中去掉了3月2日与3月28日的两组数据,请根据这5天中的另三天的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若由线性回归方程得到的估计数据与所去掉的试验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
(参考公式: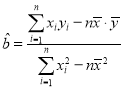 ,
,![]() )(参考数据:
)(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图和90后从事互联网行业者岗位分布图(90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生),则下列结论中不一定正确的是( )
整个互联网行业从业者年龄分布饼状图 90后从事互联网行业者岗位分布图


A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数90后比80后多
C.互联网行业中从事设计岗位的人数90后比80前多
D.互联网行业中从事市场岗位的90后人数不足总人数的10%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点F为抛物线C:![]() (
(![]() )的焦点,过点F的动直线l与抛物线C交于M,N两点,且当直线l的倾斜角为45°时,
)的焦点,过点F的动直线l与抛物线C交于M,N两点,且当直线l的倾斜角为45°时,![]() .
.
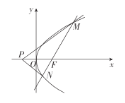
(1)求抛物线C的方程.
(2)试确定在x轴上是否存在点P,使得直线PM,PN关于x轴对称?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于具有相同定义域D的函数![]() 和
和![]() ,若存在函数
,若存在函数![]() (k,b为常数),对任给的正数m,存在相应的
(k,b为常数),对任给的正数m,存在相应的![]() ,使得当
,使得当![]() 且
且![]() 时,总有
时,总有![]() ,则称直线
,则称直线![]() 为曲线
为曲线![]() 和
和![]() 的“分渐近线”.给出定义域均为
的“分渐近线”.给出定义域均为![]() 的四组函数如下:
的四组函数如下:
①![]() ,
,![]() ;
;
②![]() ,
,![]() ;
;
③![]() ,
,![]() ;
;
④![]() ,
,![]()
其中,曲线![]() 和
和![]() 存在“分渐近线”的是________.
存在“分渐近线”的是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,曲线![]() :
: ![]() 经过伸缩变换
经过伸缩变换![]() 后得到曲线
后得到曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求出曲线![]() 、
、![]() 的参数方程;
的参数方程;
(Ⅱ)若![]() 、
、![]() 分别是曲线
分别是曲线![]() 、
、![]() 上的动点,求
上的动点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某芯片公司对今年新开发的一批5G手机芯片进行测评,该公司随机调查了100颗芯片,并将所得统计数据分为![]() 五个小组(所调查的芯片得分均在
五个小组(所调查的芯片得分均在![]() 内),得到如图所示的频率分布直方图,其中
内),得到如图所示的频率分布直方图,其中![]() .
.

(1)求这100颗芯片评测分数的平均数(同一组中的每个数据可用该组区间的中点值代替).
(2)芯片公司另选100颗芯片交付给某手机公司进行测试,该手机公司将每颗芯片分别装在3个工程手机中进行初测。若3个工程手机的评分都达到11万分,则认定该芯片合格;若3个工程手机中只要有2个评分没达到11万分,则认定该芯片不合格;若3个工程手机中仅1个评分没有达到11万分,则将该芯片再分别置于另外2个工程手机中进行二测,二测时,2个工程手机的评分都达到11万分,则认定该芯片合格;2个工程手机中只要有1个评分没达到11万分,手机公司将认定该芯片不合格.已知每颗芯片在各次置于工程手机中的得分相互独立,并且芯片公司对芯片的评分方法及标准与手机公司对芯片的评分方法及标准都一致(以频率作为概率).每颗芯片置于一个工程手机中的测试费用均为300元,每颗芯片若被认定为合格或不合格,将不再进行后续测试,现手机公司测试部门预算的测试经费为10万元,试问预算经费是否足够测试完这100颗芯片?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com