
【题目】已知函数f(x)= 
(1)当x≤0时,解不等式f(x)≥﹣1;
(2)写出该函数的单调区间;
(3)若函数g(x)=f(x)﹣m恰有3个不同零点,求实数m的取值范围.
【答案】
(1)解:当x≤0时, ![]() ,
,
解得x≥﹣1,
综上,﹣1≤x≤0,
故解集为[﹣1,0]
(2)解:函数f(x)的图象如右图,
函数f(x)的单调递减区间是(0,1),
单调增区间是(﹣∞,0)及(1,+∞)
(3)解:作出直线y=m,
函数g(x)=f(x)﹣m恰有3个不同零点等价于
函数y=m与函数f(x)的图象恰有三个不同公共点.
由函数 
又f(0)=1, ![]() ,
,
∴ ![]() .
.
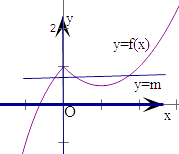
【解析】(1)由x≤0时的函数表达式,通过指数函数的单调性解出不等式即可;(2)画出函数f(x)的图象,通过图象观察即可;(3)作出直线y=m,函数g(x)=f(x)﹣m恰有3个不同零点等价于函数y=m与函数f(x)的图象恰有三个不同公共点.由图象观察即可得到.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E,F,G,H分别为AA1 , AB,BB1 , B1C1的中点,则异面直线EF与GH所成的角等于( ) 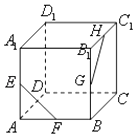
A.45°
B.60°
C.90°
D.120°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商人投资81万元建一间工作室,第一年装修费为1万元,以后每年增加2万元,把工作室出租,每年收入租金30万元.
(1)若扣除投资和各种装修费,则从第几年开始获取纯利润?
(2)若干年后该商人为了投资其他项目,对该工作室有两种处理方案:①年平均利润最大时,以46万元出售该工作室;②纯利润总和最大时,以10万元出售该工作室.问该商人会选择哪种方案?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2-lnx。
(Ⅰ)当a=![]() 时,判断f(x)的单调性;(Ⅱ)设f(x)≤x3+4x-lnx,在定义域内恒成立,求a的取值范围。
时,判断f(x)的单调性;(Ⅱ)设f(x)≤x3+4x-lnx,在定义域内恒成立,求a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ax2﹣(2a+1)x+2lnx(a≥0)
ax2﹣(2a+1)x+2lnx(a≥0)
(1)当a=0时,求f(x)的单调区间;
(2)求y=f(x)在区间(0,2]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=ax3+bx2+cx的极小值为﹣8,其导函数y=f′(x)的图象经过点 ![]() ,如图所示,
,如图所示, 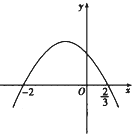
(1)求f(x)的解析式;
(2)若对x∈[﹣3,3]都有f(x)≥m2﹣14m恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界.已知函数 ![]() .
.
(1)若f(x)是奇函数,求m的值;
(2)当m=1时,求函数f(x)在(﹣∞,0)上的值域,并判断函数f(x)在(﹣∞,0)上是否为有界函数,请说明理由;
(3)若函数f(x)在[0,1]上是以3为上界的函数,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com