
【题目】某几何体的三视图如图所示(单位:cm),则该几何体的表面积是cm2 , 体积是cm3 . 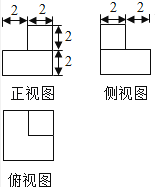
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在学习过程中,我们通常遇到相似的问题.
(1)已知动点![]() 为圆
为圆![]() :
: ![]() 外一点,过
外一点,过![]() 引圆
引圆![]() 的两条切线
的两条切线![]() 、
、![]() .
. ![]() 、
、![]() 为切点,若
为切点,若![]() ,求动点
,求动点![]() 的轨迹方程;
的轨迹方程;
(2)若动点![]() 为椭圆
为椭圆![]() :
: ![]() 外一点,过
外一点,过![]() 引椭圆
引椭圆![]() 的两条切线
的两条切线![]() 、
、![]() .
. ![]() 、
、![]() 为切点,若
为切点,若![]() ,猜想动点
,猜想动点![]() 的轨迹是什么,请给出证明并求出动点
的轨迹是什么,请给出证明并求出动点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为![]() 的函数
的函数![]() 同时满足以下三个条件:
同时满足以下三个条件:
①对任意的![]() ,总有
,总有![]() ;
;
②![]() ;
;
③若![]() ,
,![]() 且
且![]() ,则有
,则有![]() 成立,则称
成立,则称![]() 为“友谊函数”.
为“友谊函数”.
(![]() )若已知
)若已知![]() 为“友谊函数”,求
为“友谊函数”,求![]() 的值.
的值.
(![]() )分别判断函数
)分别判断函数![]() 与
与![]() 在区间
在区间![]() 上是否为“友谊函数”,并给出理由.
上是否为“友谊函数”,并给出理由.
(![]() )已知
)已知![]() 为“友谊函数”,且
为“友谊函数”,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,已知点A(1,0,B(-1,0),圆![]() 的方程为
的方程为![]() ,点
,点![]() 为圆上的动点.
为圆上的动点.
(1)求过点![]() 的圆
的圆![]() 的切线方程.
的切线方程.
(2)求![]() 的最大值及此时对应的点
的最大值及此时对应的点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图如图所示,考虑以下结论:
甲 | 乙 | ||||||||
8 | 0 | ||||||||
4 3 3 | 6 6 8 | 3 8 9 1 | 1 2 3 4 5 | 2 5 1 4 0 | 5 4 6 9 | 1 | 6 | 7 | 9 |
①甲运动员得分的中位数大于乙运动员
得分的中位数;
②甲运动员得分的中位数小于乙运动员
得分的中位数;
③甲运动员得分的标准差大于乙运动员
得分的标准差;
④甲运动员得分的标准差小于乙运动员
得分的标准差;
其中根据茎叶图能得到的正确结论的编号为( )
A. ①③ B. ①④
C. ②③ D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com