
 =2
=2 ,P是平面内一动点,且满足|
,P是平面内一动点,且满足| |•|
|•| |=
|= •
• .
.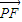 |•|
|•| |=
|=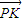 •
•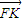 ,即可求P点的轨迹C的方程;
,即可求P点的轨迹C的方程;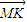 =2
=2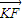 ,
,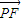 |•|
|•|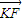 |=
|=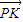 •
•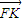 ,
,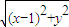 =(-1-x,-y)•(-2,0)
=(-1-x,-y)•(-2,0)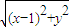 =1+x,即y2=4x;
=1+x,即y2=4x;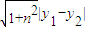 =4(n2+1)
=4(n2+1)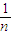 y+1,与y2=4x联立,
y+1,与y2=4x联立,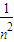 +1)
+1) |AB||DE|=8(n2+1)(
|AB||DE|=8(n2+1)( +1)=8(n2+
+1)=8(n2+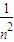 +2)≥32
+2)≥32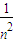 ,即n=±1时,四边形ADBE的面积的最小值为32.
,即n=±1时,四边形ADBE的面积的最小值为32.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
| MC |
| PC |
| BC |
| PB |
| CB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| MK |
| KF |
| PF |
| KF |
| PK |
| FK |
查看答案和解析>>
科目:高中数学 来源:重庆模拟 题型:解答题
| MC |
| PC |
| BC |
| PB |
| CB |
查看答案和解析>>
科目:高中数学 来源:2009-2010学年重庆市重点高中联盟高三联考数学试卷(理科)(解析版) 题型:解答题
 所成的比为2.P是平面上一动点,且满足
所成的比为2.P是平面上一动点,且满足 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com