
 为三条不同的直线,
为三条不同的直线, 为一个平面,下列命题中不正确的是( )
为一个平面,下列命题中不正确的是( )A.若 ,则 ,则 与 与 相交 相交 |
B.若 则 则 |
C.若  // //  , , // //  , , ,则 ,则 |
D.若 // //  , ,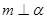 , , ,则 ,则 // //  |
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com